ML Aggarwal Class 9 Logarithms Chapter Test

ML Aggarwal Class 9 Solutions Chapter 9 Chapter Test

Question 1.
Expand \(\log _{a} \sqrt[3]{x^{7} y^{8} \div \sqrt[4]{z}}\)
Answer:

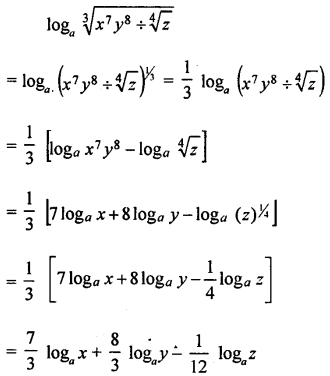
Question 2.
Find the value of \(\log _{\sqrt{3}} 3 \sqrt{3}-\log _{5}(0 \cdot 04)\)
Answer:

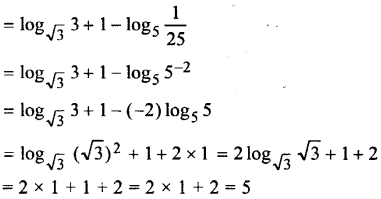
Question 3.
Prove the following

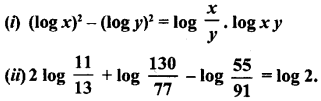
Answer:

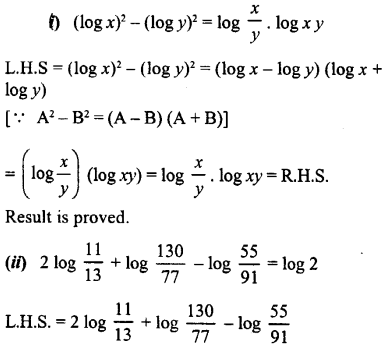
= 2[log 11 – log 13] + [log 130 – log 77] – [log 55 – log 91]
= 2 [log – log 13] + [log 13 × 10 – log 11 × 7] – [log 11 – log 13 × 7]
= 2 [log 11 – log 13] + [(log 13 + log 10) – (log 11 + log 7)] – [(log 11 + log 5) – (log 13 + log 7)]
= 2 log 11 – 2 log 13 + log 10 – log 11 – log 7 – log 11 – log 5 + log 13 + log 7
= (2 log 11 – log 11 – log 11) + (-2 log 13 + log 13 + log 13) + log 10 – log 5 + (log 7 – log 7)
= 0 + 0 + log 10 – log 5 + 0 = log 10 – log 5
= log\(\left(\frac{10}{5}\right)\) = 1og 2 = R.H.S
Hence, Result is proved.

Question 4.
If log (m + n) = log m + log n, show that n = \(\frac{m}{m-1}\).
Answer:
Given log (m + n) = log m + log n
⇒ log (m + n) = log mn ⇒ m + n = mn
⇒ m = mn – n ⇒ m = n (m -1)
⇒ n (m – 1) = m ⇒ n = \(\frac{m}{m-1}\)
Hence, result is proved.

Question 5.
If \(\log \frac{x+y}{2}=\frac{1}{2}(\log x+\log y)\), prove that x = y.
Answer:

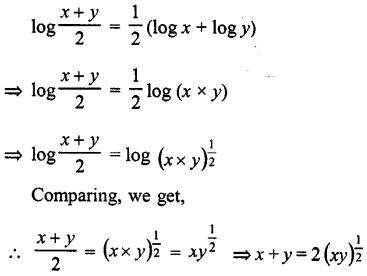
Squaring
⇒ (x + y)² = 4xy ⇒ x² + y² + 2xy = 4xy
⇒ x² + y² + 2xy – 4xy = 0 ⇒ x² + y² – 2xy = 0
⇒ (x – y)² = 0 ⇒ x – y = 0
∴ x = y Hence proved.

Question 6.
If a, b are positive real numbers, a > b and a² + b² = 27 ab, prove that

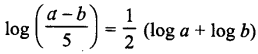
Answer:
a² + b² = 27ab
⇒ a² + b² – 2ab = 25ab


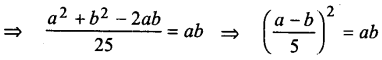
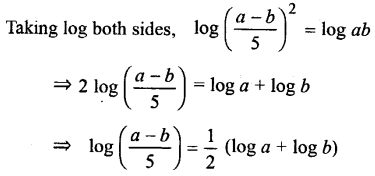
Hence proved.
Solve the following equations for x

Question 7.
Solve the following equations for x:
(i) log_x\(\frac{1}{49}\) = -2
(ii) log_x\(\frac{1}{4 \sqrt{2}}\) = -5
(iii) log_x\(\frac{1}{243}\) = 10
(iv) log_x32 = x – 4
(v) log₇ (2x² – 1) = 2
(vi) log (x² – 21) = 2
(vii) log₆ (x – 2) (x + 3) = 1
(viii) log₆ (x – 2) + log₆ (x + 3) = 1
(ix) log (x +1) + log (x -1) = log 11 + 2 log 3.
Answer:


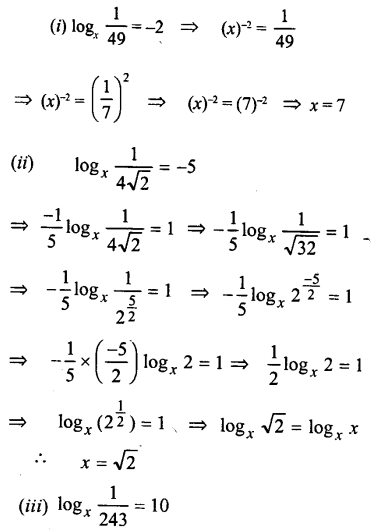
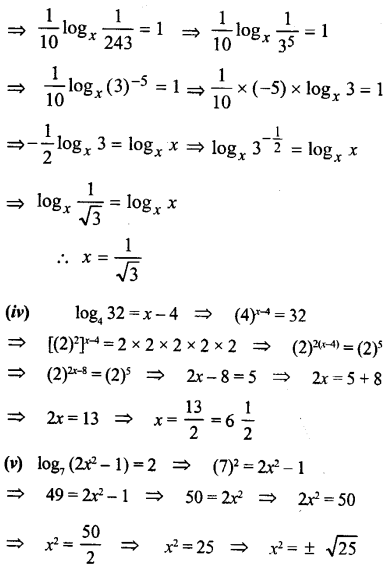
⇒ x = +5, -5

(vi) log (x² – 21) = 2
(10)² = x² – 21 ⇒ 100 = x² – 21
⇒ x² – 21 = 100 ⇒ x² = 100 + 21
⇒ x² = 121 ⇒ x = ±\(\sqrt{121}\) ⇒ x = ±11
∴ x = 11, -11

(vii) log₆ (x – 2) (x + 3) = 1 {∵ log_a a= 1}
Comparing,
(x – 2)(x + 3) = 6
⇒ x² + 3x – 2x – 6 = 6
⇒ x² + x – 6 – 6 = 0
⇒ x² + x- 12 = 0
⇒ x² + 4x – 3x- 12 = 0
⇒ x (x + 4) – 3 (x + 4) = 0
⇒ (x + 4)(x – 3) = 0
Either x + 4 = 0, then x = -4
or x – 3 = 0, then x = 3
Hence x = 3, -4

(viii) log₆ (x – 2) + log₆ (x + 3) = 1
log₆ (x – 2) (x + 3) = 1 = log₆ 6 {∵ log_a a = 1}
Comparing,
(x – 2) (x + 3) = 6 => x² + 3x – 2x – 6 = 6
⇒ x² + x – 6 – 6 = 0 ⇒ x² + x – 12 = 0
⇒ x² + 4x – 3x – 12 = 0
⇒ x (x + 4) – 3 (x + 4) = 0
⇒ (x + 4)(x – 3) = 0
Either x + 4 = 0, then x = -4
or x – 3 = 0, then x = 3
∴ x = 3, -4

(ix) log (x +1) + log (x -1) = log 11 + 2 log 3
⇒ log [(x + 1) (x – 1)] = log 11 + log (3)²
⇒ log (x² – 1) = log 11 + log 9 [∵ a² – b² = (a + b)(a – b)]
⇒ log(x² – 1) = log(11 × 9) ⇒ x² – 1 = 11 × 9
⇒ x² – 1 = 99 × x² = 99 + 1 ⇒ x² = 100
⇒ x² = (10)2² ⇒ x = 10

Question 8.
Solve for x and y:

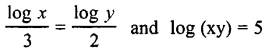
Answer:

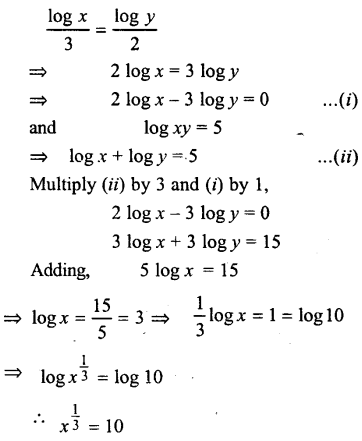
Question 9.
If a = 1 + log_xyz, b = 1 + log_y zx and c = 1 + log_zxy, then show that ab + bc + ca = abc.
Answer:
a = 1 + log_xyz
b = 1 + log_yzx
c = 1 + log_zxy
a = 1 + log_xyz = log_xx + log_xyz

ML Aggarwal Class 9 Solutions for ICSE Maths