ML Aggarwal Class 9 Solutions Chapter 3 Chapter Test
Question 1.
Find the expansions of the following :
(i) (2x + 3y + 5) (2x + 3y – 5)
(ii) (6 – 4a -7b)2
(iii) (7 – 3xy)3
(iv) (x + y + 2)3
Answer:
(i) (2x + 3y + 5) (2x + 3y – 5) = [(2x + 3y) + 5] [(2x -3y) – 5]
= (2x + 3y)2 – (5)2
= (2x)2 + (3y) 2 + 2 × 2x × 3y – 5 × 5
= 4x2 + 9y2 + 12xy -25
(ii) (6 – 4a – 7 b)2 = [ 6 + (- 4a) + (-7b)]2
= (6)2 + (- 4a)2 + (- 7b)2 + 2 (6) (- 4a) + 2 (- 4a) (-7b)+ 2 (-7b) (6) .
= 36 + 16a2 + 49b2 – 48a + 56ab – 84b
(iii) (7 – 3xy)3
= (7)3 – (3xy)3 – 3 (7) (3xy) (7 – 3xy)
⇒ (7 – 3xy)3 = 343 – 27x3y3 – 63xy (7 – 3xy)
⇒ (7 – 3xy)3 = 343 – 27x3y3 – 441xy + 189x2y2
(iv) (x + y + 2 )3 = [(x + y) + 2]3
= (x + y)3 + (2)3 + 3 (x + y) (2) (x + y + 2)
= x3 + y3 + 3x2y + 3xy2 + 8 + 6 (x + y) [(x + y) + 2]
= x3 + y3 + 3x2y + 3xy2 + 8 + 6 (x + y)2 +12(x + y)
= x3 + y3 + 3x2y + 3xy2 + 8 + 6 (x2 + y2 + 2xy) + 12x + 12y = x3 + y3 + 3x2y + 3xy2 + 8 + 6x2 + 6y2 + 12xy + 12x + 12y
= x3 + y3 + 3x2y + 3xy2 + 8 + 6x2 + 6y2 + 12x + 12y + 12xy
Question 2.
Simplify (x – 2) ( x + 2)(x2 + 4) (x4 + 16)
Answer:
(x – 2) (x + 2) (x4 + 4) (x4 +16)
= (x2 – 4) (x4 + 4) ( x4 + 16)
= [(x2)2 – (4)2] (x4 + 16)
= (x4 – 16) (x4 + 16) = (x4)2 – (16)2 = x8 – 256
Question 3.
Evaluate 1002 × 998 by using a special product.
Answer:
1002 × 998 = (1000 + 2) (1000 – 2)
= (1000)2 – (2)2 = 1000000 – 4 = 999996.
Question 4.
If a + 2b + 3c = 0 , Prove that a3 + 8b3 + 27c3 = 18 abc
Answer:
Given a + 2b + 3c = 0, a + 2b = – 3c
On cubing both sides, we get (a + 2b)3
= (-3c)3
⇒ a3 + (2b)3 + 3(a) (2b) (a + 2b) = -27c3
⇒ a3 + 8b3 + 6ab ( – 3c) = – 27c3
⇒ a3 + 8b3 – 18abc = -27c3
⇒ a3 + 8b3 + 27c3 = 18abc.
Question 5.
If 2x = 3y – 5, then find the value of 8x3 – 27y3 + 90xy + 125.
Answer:
2x = 3y – 5
⇒ 2x – 3y = -5
Cubing both sides (2x – 3y)3 = (-5)3
(2x)3 – (3y)3 – 3 × 2x × 3y (2x – 3y) = -125
⇒ 8x3 – 27y3 – 18xy (2x – 3y) = -125
⇒ 8x3 – 27y3 – 18xy (-5) = -125 (∵ 2x -3y = -5)
⇒ 8x3 – 27y3 + 90xy = -125
⇒ 8x3 – 27y3 + 90xy + 125 = 0
Question 6.
If a2−1a2=5, evaluate a4+1a4
Answer:
We know that,
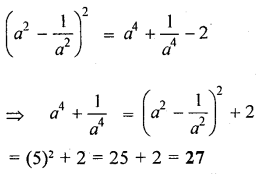
Question 7.
If a+1a=p and a−1a=q, Find the relation between p and q
Answer:
We know that,
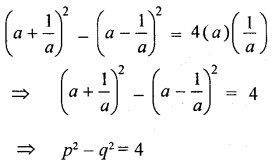
Which is the required relation between p and q.
Question 8.
If a2+1a=4, find the value of 2a3+2a3.
Answer:
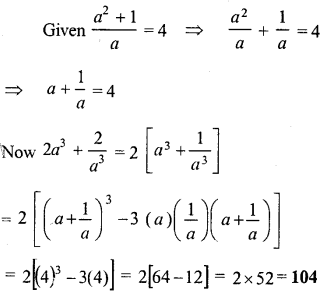
Question 9.
If x=14−x, find the value of
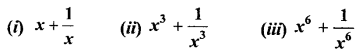
Answer:

Question 10.
If x−1x=3+2√2, find the value of
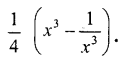
Answer:
![]()
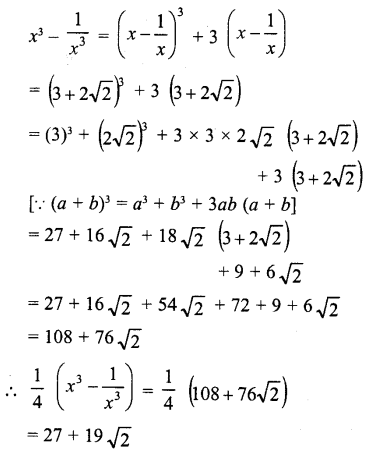
Question 11.
If x+1x=313, Find the value of x3−1x3.
Answer:
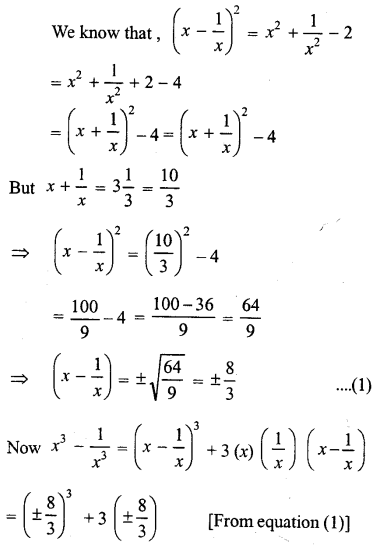
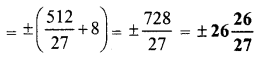
Question 12.
If x=2−√3, then find the value of x3−1x3.
Answer:
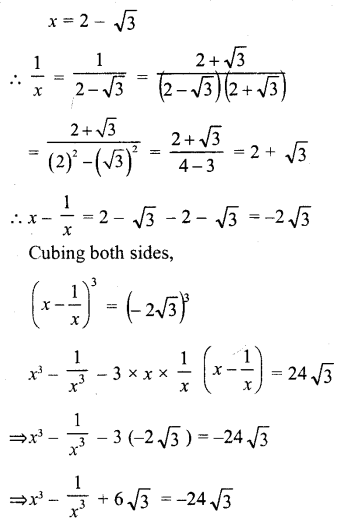
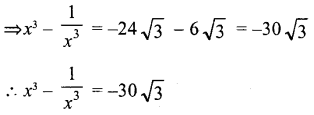
Question 13.
If the sum of two numbers is 11 and sum of their cubes is 737, find the sum of their squares.
Answer:
Let x and y be the two numbers, then
x + y = 11
x3 + y3 = 735 and x2 + y2 = ?
x + y = 11
Cubing both sides,
(x + y)3 = (11)3
⇒ x3 + y3 + 3xy (x + y) = 1331
⇒ 737 + 3x × 11 = 1331
⇒ 33xy = 1331 – 737 = 594
xy = 59433 = 8
Now ∵ x + y = 11
Squaring both sides,
(x + y)2 = (11)2
⇒ x2 + y2 + 2xy = 121 2 x2 + y2 + 2 × 18 = 121
⇒ x2 + y2 + 36 = 121
⇒ x2 + y2 = 121 – 36 = 85
Hence sum of the squares = 85
Question 14.
If a – b = 7 and a3 – b3 = 133, find :
(i) ab
(ii) a2 + b2
Answer:
a – b = 7
Cubing both sides,
(i) (a – b)3 = (7)3
⇒ a3 + b3 – 3ab (a – b) = 343
⇒ 133 – 3ab × 7 = 343
⇒ 133 – 21ab = 343
⇒ – 21ab = 343 – 133 21ab = 210
⇒ ab = 210−21 = -10
(ii) Again a – b = 7 Squaring both sides,
(a – b)2 = (7)2
⇒ a2 + b2 – 2ab = 49
⇒ a2 + b2 – 2 × (- 10) = 49
⇒ a2 + b2 + 20 = 49
⇒ a2 + b2 = 49 – 20 = 29
Hence a2 + b2 = 29
Question 15.
Find the coefficient of x2 expansion of (x2 + x + 1)2 + (x2 – x + 1)2
Answer:
Given expansion
= (x2 + x + 1)2 + (x2 – x + 1)2
= [(x2 + 1) + x2 + [(x2 + 1) – x)2
= (x2 + 1)2 + x2 + 2 (x2 + 1) (x) + (x2 + 1)2 + x2 – 2 (x2 + 1) (x)
= (x2)2 + (1)2 + 2 × x2 × 1 + x2 + (x2)2 + 1 + 2 × x2 + 1 + x2
= x42 + 1 + 2x22 + x2 + x4 + 1 + 2x2 + x2
= 2x4 + 6x2 + 2
∴ Co-efficient of x2 = 6
