ML Aggarwal Class 9 Trigonometric Ratios Chapter Test

ML Aggarwal Class 9 Solutions Chapter 17 Chapter Test

Question 1.
(a) From the figure (i) given below, calculate all the six t-ratio for both acute angles.
(b) From the figure (ii) given below, find the values of x and y in terms of t-ratio of θ.

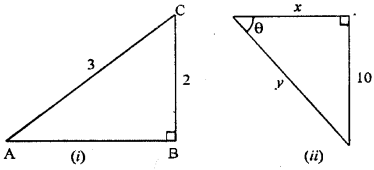
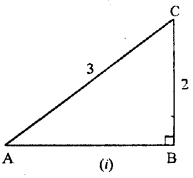
Answer:
Given ∆ ABC is right angled at B,
Then in right angled ∆ ABC,
By Pythagoras theorem, we get
AC² = AB² + BC²
⇒ AB² = AC² – BC²
⇒ AB² = (3)² – (2)²
⇒ AB² = 9 – 4
⇒ AB² = 5
AB = $\sqrt5$



(b) Let ABC be given triangle in which B is at right angle and ∠ BAC = θ
Then we know that,

Question 2.
(a) From the figure (1) given below, find the values of:
(i) sin ∠ ABC
(ii) tanx – cosx + 3sinx.
(b) From the figure (2) given below, find the values of;
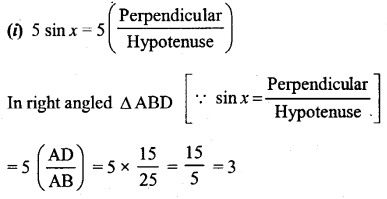
(i) 5 sin x
(ii) 7 tan x
(iii) 5 cos x – 17 siny – tan x.

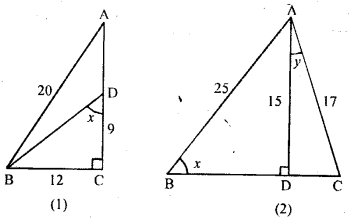
Answer:
(a) In this figure
BC = 12, CD = 9 and BC = 20
In right angled ∆ ABC,

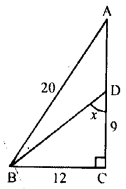
By Pythagoras theorem, we get
AB² = AC² + BC²
⇒ ² = AB² – BC²
⇒ AC² = (20)² – (12)²
⇒ AC² = 400 – 144
⇒ AC² = 256 ⇒ AC² = (16)² ⇒ AC = 16
But, In right angled ∆ BCD,
By Pythagoras theorem, we get
BD² = ² + CD²
⇒ BD² = (12)² + (9)²
BD²= 144 + 81 ⇒ BD² = 225 ⇒ BD² = (15)²
⇒ BD = 15


(b) From figure AC = 17, AB = 25, AD = 15
In right angled ∆ ACD By Pythagoras theorem, we get

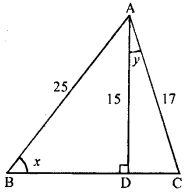
AC² = AD² + CD(17)² = (15)² + (CD)²
⇒ CD² = (17)² – (15)²
⇒ CD² = 289 – 225
⇒ CD² = 64
⇒ CD² = (8)²
⇒ CD = 8
In right angled ∆ABD,
By Pythagoras theorem, we get ,
AB² = AD² + BD²
⇒ (25)² = (15)² + BD² ⇒ BD² = (25)² – (15)²
⇒ BD² = 625 – 225 ⇒ BD² = 400
⇒ BD² = (20)² ⇒ BD = 20

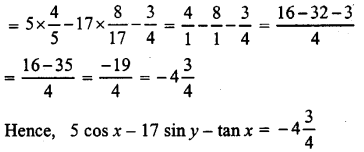
Question 3.
If q cosθ = p, find tan θ – cot θ in terms of p and q.
Answer:
Let ABC be a right angled triangle and B at right angled and ∠ ACB = 0 .

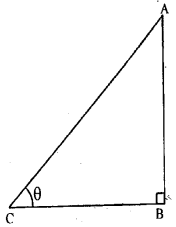
Given that,
q cos θ = p ⇒ cos θ = $\frac{p}{q}$
⇒ $\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{p}{q}$
Let BC = px then AC = qx
In right angled ∆ ABC,
By Pythagoras theorem, we get
AC² = AB² + BC²
⇒ AB² = AC² – BC²
⇒ AB² = (qx)² – (px)²
⇒ AB² = q²x² – p²x²
⇒ AB² = (q² – p²) x²

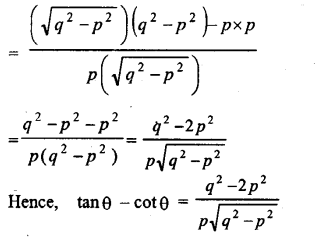
Question 4.
Given 4 sin θ =3 cos θ, find the values of :
(i) sin θ
(ii) cos θ
(iii) cot² θ – cosec² θ.
Answer:
Given that, 4sin θ = 3cosθ
⇒ $\frac{\sin \theta}{\cos \theta}=\frac{3}{4}$

Question 5.
If 2 cos θ = $\sqrt3$, prove that 3 sin θ – 4 sin³ θ = 1
Answer:
2 cos θ = $\sqrt3$

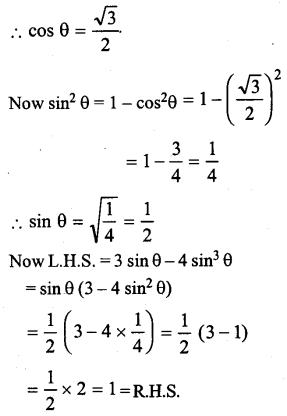
Hence proved.

Question 6.
If $\frac{\sec \theta-\tan \theta}{\sec \theta+\tan \theta}=\frac{1}{4}, \text { find } \sin \theta$
Answer:

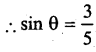
Question 7.
If sin θ + cosec θ = $3 \frac{1}{3}$, find the value of sin² θ + cosec² θ.
Answer:

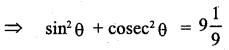
Question 8.
In the adjoining figure, AB = 4 m and ED = 3 m.
If sin α = $\frac{3}{5}$ and cos β = $\frac{12}{13}$ , And the length of BD.

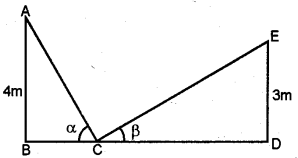
Answer:
sin α = $\frac{3}{5}$ = $\frac{AB}{AC}$
∴ AB = 3, AC = 5
But AC² = AB² + BC²
⇒ (5)² = (3)² + BC² ⇒ 25 = 9 + BC²
⇒ BC² = 25 – 9 = 16 = (4)^-2 ⇒ BC = 4
∴ tan α = $\frac{AB}{BC}$ = $\frac{4}{5}$
cos β = $\frac{12}{13}$ = $\frac{CD}{CE}$
∴ CD = 12, CE = 13
But CE² = CD² + ED²
(13)² = (12)² + (ED)²
⇒ 169 = 144 + ED² ⇒ ED² = 169 – 144 = 25 = (5)²
∴ ED = 5

ML Aggarwal Class 9 Solutions for ICSE Maths