Pythagoras Theorem Class 9 ICSE ML Aggarwal

ML Aggarwal Class 9 Solutions Chapter 12 provides comprehensive guidance and step-by-step explanations for the concepts covered in this chapter Class 9 Mathematics. This chapter typically introduces fundamental mathematical concepts, laying the groundwork for future studies.

ML Aggarwal Class 9 Chapter 12 Solutions

ICSE Class 9 Maths Chapter 12 Solutions ML Aggarwal

Question 1.
Lengths of sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse:
(i) 3 cm, 8 cm, 6 cm
(ii) 13 cm, .12 cm, 5 cm
(iii) 1.4 cm, 4.8 cm, 5 cm
Solution:

Question 2.
Foot of a 10 m long ladder leaning against a vertical well is 6 m away from the base of the wail. Find the height of the point on the wall where the top of the ladder reaches.
Solution:

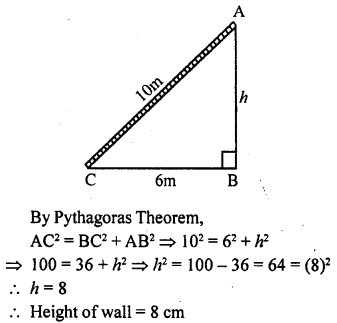
Question 3.
A guy attached a wire 24 m long to a vertical pole of height 18 m and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taught?
Solution:

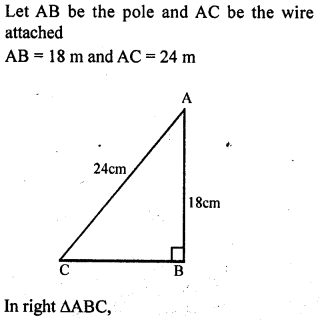
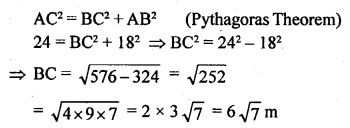
Question 4.
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
Solution:

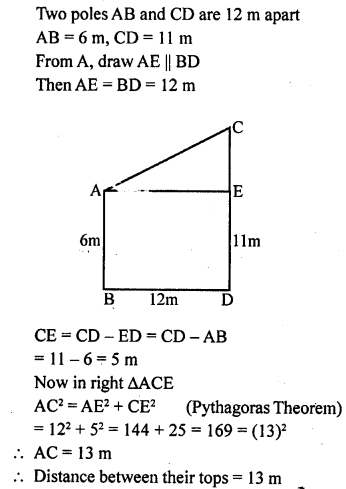
Question 5.
In a right-angled triangle, if hypotenuse is 20 cm and the ratio of the other two sides is 4:3, find the sides.
Solution:

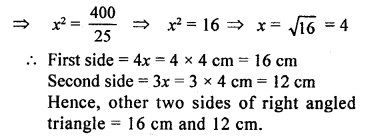
Question 6.
If the sides of a triangle are in the ratio 3:4:5, prove that it is right-angled triangle.
Solution:

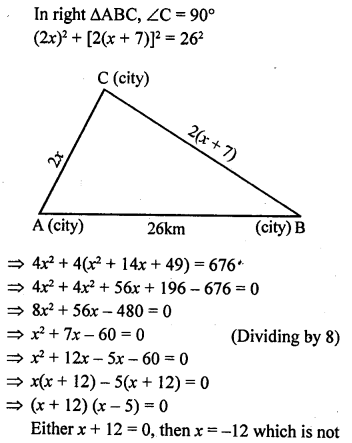
Question 7.
For going to a city B from city A, there is route via city C such that AC ⊥ CB, AC = 2x km and CB=2(x+ 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of highway.
Solution:

Question 8.
The hypotenuse of right triangle is 6m more than twice the shortest side. If the third side is 2m less than the hypotenuse, find the sides of the triangle.
Solution:

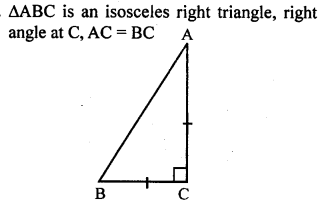
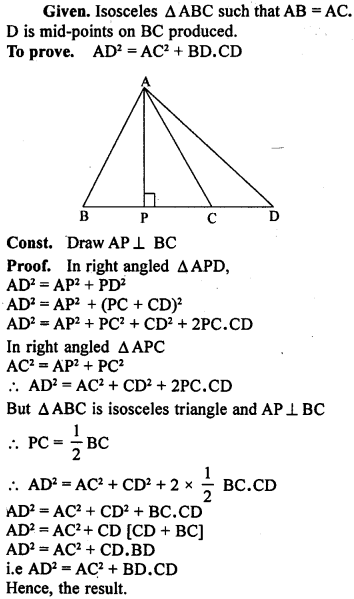
Question 9.
ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC².
Solution:

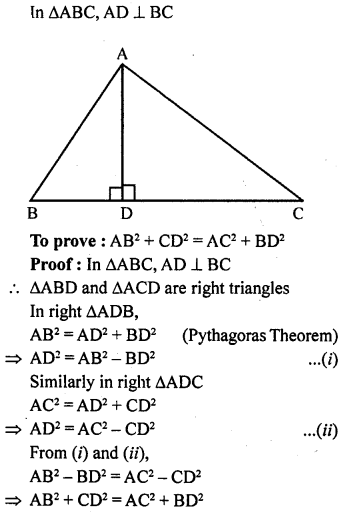
Question 10.
In a triangle ABC, AD is perpendicular to BC. Prove that AB² + CD² = AC² + BD².
Solution:

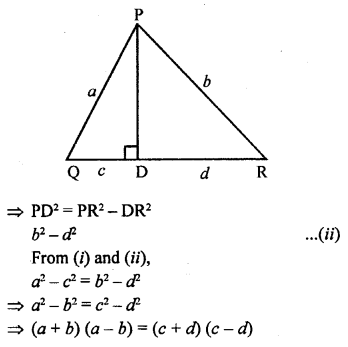
Question 11.
In ∆PQR, PD ⊥ QR, such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b) (a – b) = (c + d) (c – d).
Solution:

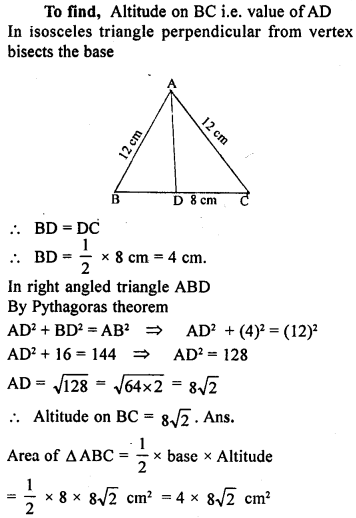
Question 12.
ABC is an isosceles triangle with AB = AC = 12 cm and BC = 8 cm. Find the altitude on BC and Hence, calculate its area.
Solution:

Question 13.
Find the area and the perimeter of a square whose diagonal is 10 cm long.
Solution:

Question 14.
(a) In fig. (i) given below, ABCD is a quadrilateral in which AD = 13 cm, DC = 12 cm, BC = 3 cm, ∠ ABD = ∠BCD = 90°. Calculate the length of AB.
(b) In fig. (ii) given below, ABCD is a quadrilateral in which AB = AD, ∠A = 90° =∠C, BC = 8 cm and CD = 6 cm. Find AB and calculate the area of ∆ ABD.

Solution:

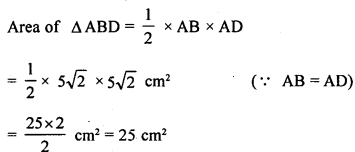
Question 15.
(a) In figure (i) given below, AB = 12 cm, AC = 13 cm, CE = 10 cm and DE = 6 cm.Calculate the length of BD.
(b) In figure (ii) given below, ∠PSR = 90°, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.
(c) In figure (iii) given below, ∠ D = 90°, AB = 16 cm, BC = 12 cm and CA = 6 cm. Find CD.

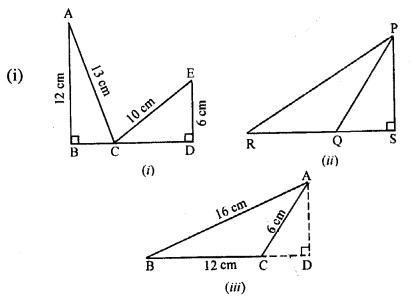
Solution:

Question 16.
(a) In figure (i) given below, BC = 5 cm,
∠B =90°, AB = 5AE, CD = 2AE and AC = ED. Calculate the lengths of EA, CD, AB and AC.
(b) In the figure (ii) given below, ABC is a right triangle right angled at C. If D is mid-point of BC, prove that AB2 = 4AD² – 3AC².

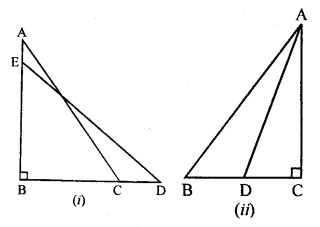
Solution:

Question 17.
In ∆ ABC, AB = AC = x, BC = 10 cm and the area of ∆ ABC is 60 cm². Find x.
Solution:

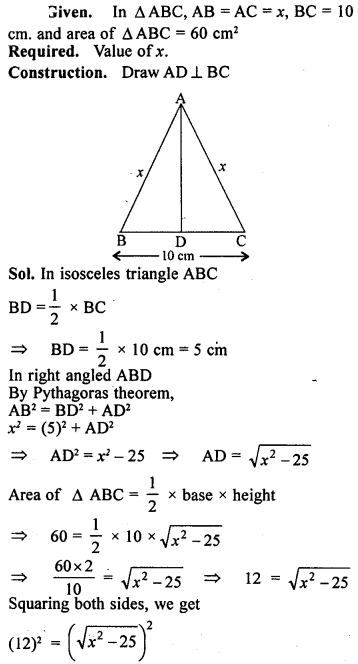
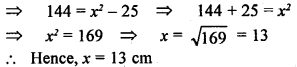
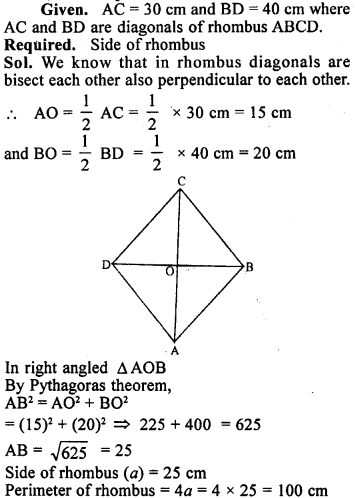
Question 18.
In a rhombus, If diagonals are 30 cm and 40 cm, find its perimeter.
Solution:

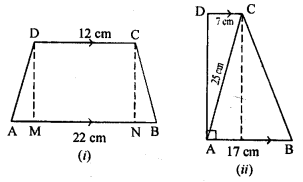
Question 19.
(a) In figure (i) given below, AB || DC, BC = AD = 13 cm. AB = 22 cm and DC = 12cm. Calculate the height of the trapezium ABCD.
(b) In figure (ii) given below, AB || DC, ∠ A = 90°, DC = 7 cm, AB = 17 cm and AC = 25 cm. Calculate BC.
(c) In figure (iii) given below, ABCD is a square of side 7 cm. if
AE = FC = CG = HA = 3 cm,
(i) prove that EFGH is a rectangle.
(ii) find the area and perimeter of EFGH.

Solution:

Question 20.
AD is perpendicular to the side BC of an equilateral Δ ABC. Prove that 4AD² = 3AB².
Solution:

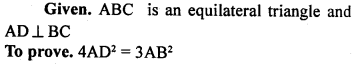
Question 21.
In figure (i) given below, D and E are mid-points of the sides BC and CA respectively of a ΔABC, right angled at C.

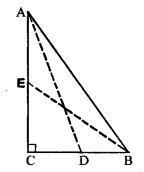
Solution:

Question 22.
If AD, BE and CF are medians of ΕABC, prove that 3(AB² + BC² + CA²) = 4(AD² + BE² + CF²).
Solution:

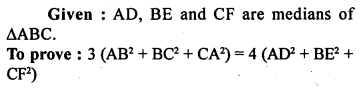
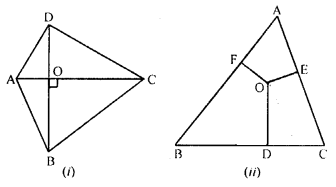
Question 23.
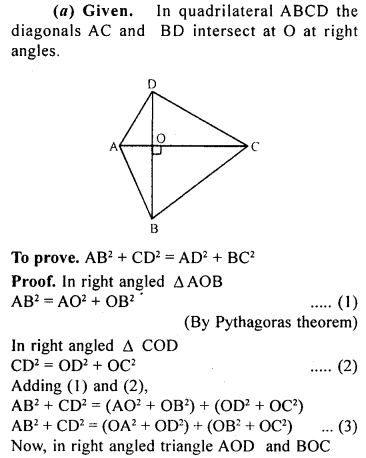
(a) In fig. (i) given below, the diagonals AC and BD of a quadrilateral ABCD intersect at O, at right angles. Prove that
AB² + CD² = AD² + BC².
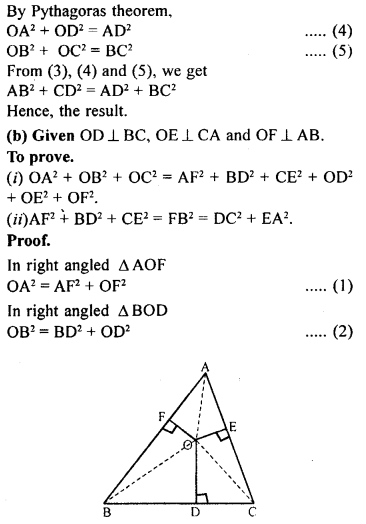
(b) In figure (ii) given below, OD⊥BC, OE ⊥CA and OF ⊥ AB. Prove that :
(i) OA² + OB² + OC² = AF² + BD² + CE² + OD² + OE² + OF².
(ii) OAF² + BD² + CE² = FB² + DC² + EA².

Solution:

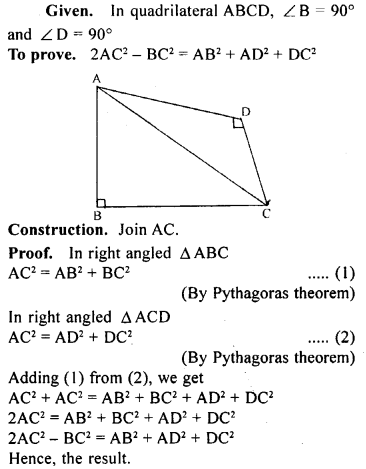
Question 24.
In a quadrilateral, ABCD∠B = 90° = ∠D. Prove that 2 AC² – BC2 = AB² + AD² + DC².
Solution:

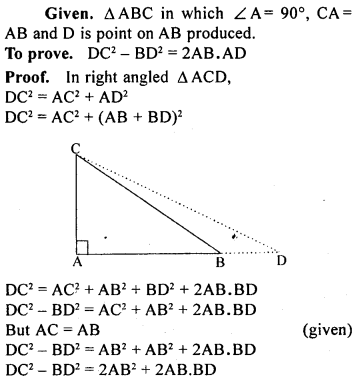
Question 25.
In a ∆ ABC, ∠ A = 90°, CA = AB and D is a point on AB produced. Prove that :
DC² – BD² = 2AB. AD.
Solution:

Question 26.
In an isosceles triangle ABC, AB = AC and D is a point on BC produced. Prove that AD² = AC² + BD.CD.
Solution:

Question P.Q.
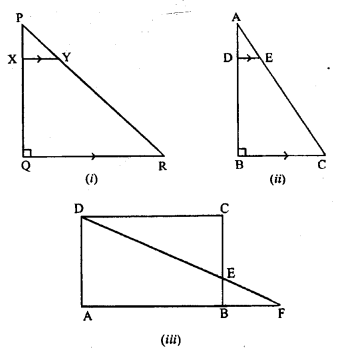
(a) In figure (i) given below, PQR is a right angled triangle, right angled at Q. XY is parallel to QR. PQ = 6 cm, PY = 4 cm and PX : OX = 1:2. Calculate the length of PR and QR.
(b) In figure (ii) given below, ABC is a right angled triangle, right angled at B.DE || BC.AB = 12 cm, AE = 5 cm and AD : DB = 1: 2. Calculate the perimeter of A ABC.
(c)In figure (iii) given below. ABCD is a rectangle, AB = 12 cm, BC – 8 cm and E is a point on BC such that CE = 5 cm. DE when produced meets AB produced at F.
(i) Calculate the length DE.
(ii) Prove that ∆ DEC ~ AEBF and Hence, compute EF and BF.

Solution:

Multiple Choice Questions

Choose the correct answer from the given four options (1 to 7):
Question 1.
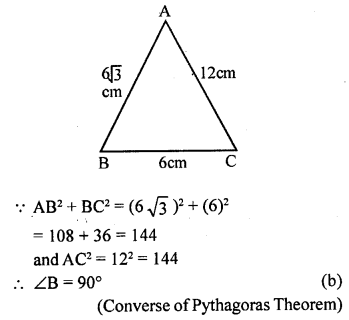
In a ∆ABC, if AB = 6√3 cm, BC = 6 cm and AC = 12 cm, then ∠B is
(a) 120°
(b) 90°
(c) 60°
(d) 45°
Solution:

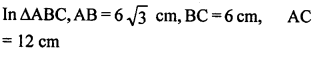
Question 2.
If the sides of a rectangular plot are 15 m and 8 m, then the length of its diagonal is
(a) 17 m
(b) 23 m
(c) 21 m
(d) 17 cm
Solution:

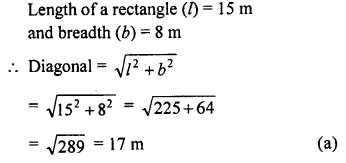
Question 3.
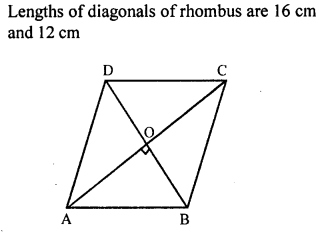
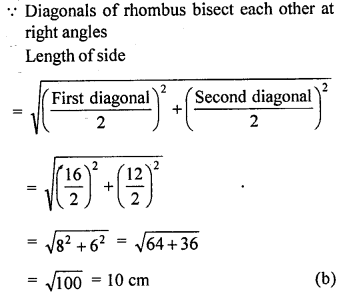
The lengths of the diagonals of a rhombus are 16 cm and 12 cm. The length of the side of the rhombus is
(a) 9 cm
(b) 10 cm
(c) 8 cm
(d) 20 cm
Solution:

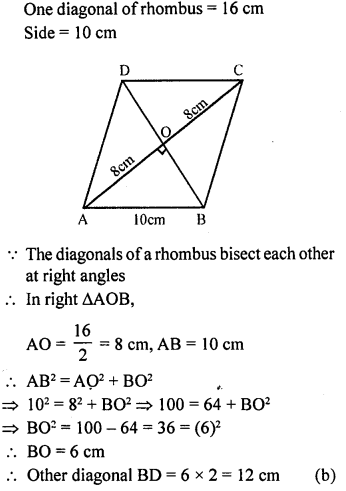
Question 4.
If a side of a rhombus is 10 cm and one of the diagonals is 16 cm, then the length of the other diagonals is
(a) 6 cm
(b) 12 cm
(c) 20 cm
(d) 12 cm
Solution:

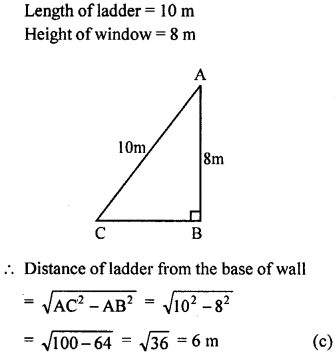
Question 5.
If a ladder 10 m long reaches a window 8 m above the ground, then the distance of the foot of the ladder from the base of the wall is
(a) 18 m
(b) 8 m
(c) 6 m
(d) 4 m
Solution:

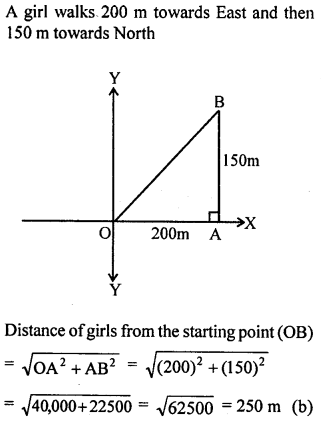
Question 6.
A girl walks 200 m towards East and then she walks ISO m towards North. The distance of the girl from the starting point is
(a) 350 m
(b) 250 m
(c) 300 m
(d) 225 m
Solution:

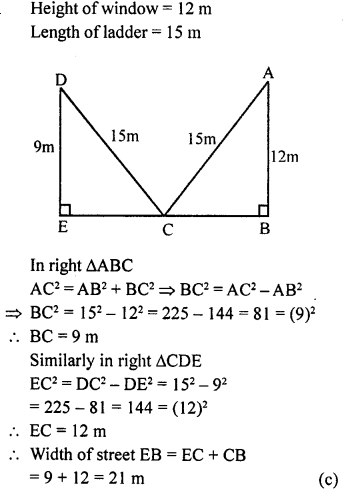
Question 7.
A ladder reaches a window 12 m above the ground on one side of the street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 9 m high. If the length of the ladder is 15 m, then the width of the street is
(a) 30 m
(b) 24 m
(c) 21 m
(d) 18 m
Solution:

Chapter Test

Question 1.
(a) In fig. (i) given below, AD ⊥ BC, AB = 25 cm, AC = 17 cm and AD = 15 cm. Find the length of BC.
(b) In figure (ii) given below, ∠BAC = 90°, ∠ADC = 90°, AD = 6 cm, CD = 8 cm and BC = 26 cm. Find :
(i) AC (ii) AB (iii) area of the shaded region.
(c) In figure (iii) given below, triangle ABC is right angled at B. Given that AB = 9 cm, AC = 15 cm and D, E are mid-points of the sides AB and AC respectively, calculate
(i) the length of BC (ii) the area of ∆ ADE.

Solution:

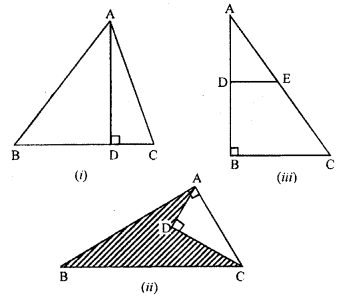
Question 2.
If in ∆ ABC, AB > AC and ADI BC, prove that AB² – AC² = BD² – CD².
Solution:

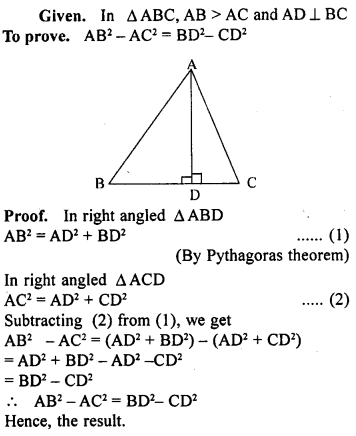
Question 3.
In a right angled triangle ABC, right angled at C, P and Q are the points on the sides CA and CB respectively which divide these sides in the ratio 2:1. Prove that
(i) 9AQ² = 9AC² + 4BC²
(ii) 9BP² = 9BC² + 4AC²
(iii) 9(AQ² + BP²) = 13AB².
Solution:
A right angled ∆ ABC in which ∠ C

Question 4.
In the given figure, ∆PQR is right angled at Q and points S and T trisect side QR. Prove that 8PT² – 3PR² + 5PS².
Solution:

Question 5.
In a quadrilateral ABCD, ∠B = 90°. If AD² = AB² + BC² + CD², prove that ∠ACD = 90°.
Solution:

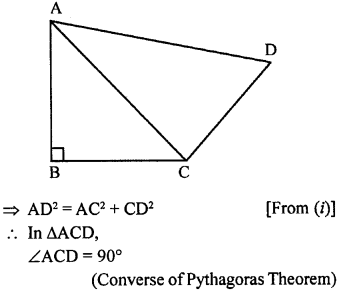
Question 6.
In the given figure, find the length of AD in terms of b and c.
Solution:

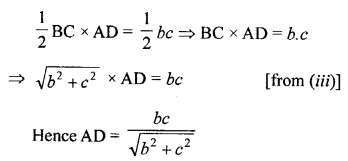
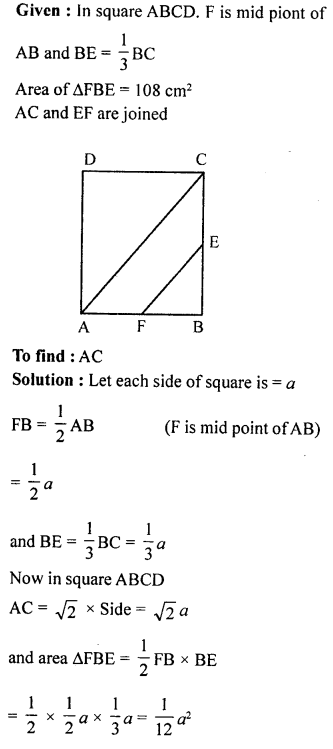
Question 7.
ABCD is a square, F is mid-point of AB and BE is one-third of BC. If area of ∆FBE is 108 cm², find the length of AC.
Solution:

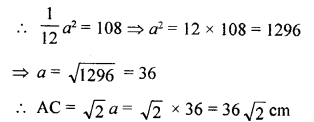
Question 8.
In a triangle ABC, AB = AC and D is a point on side AC such that BC² = AC x CD, Prove that BD = BC.
Solution: