ML Aggarwal Class 9 Rational and Irrational Numbers Chapter Test

ML Aggarwal Class 9 Solutions Chapter 1 Chapter Test

Question 1.
Without actual division, find whether the following rational numbers are terminating decimals, or recurring decimals.

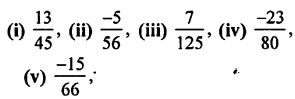
In case of terminating decimals, write their decimal expansions.
Solution:
(i) The fraction whose denominator is the multiple of 2 or 5 or both, Is a terminating decimal.
Now, in \(\frac{13}{45}\), ∵ 45 = 3 × 3 × 5

Question 2.
Express the following recurring decimals as vulgar fractions :
(i) \(1.3 \overline{45}\)
(ii) \(2 . \overline{357}\)
Solution:
(i)Let x= \(1.3 \overline{45}\) = 1.34545 …… (1)
Multiplying both sides of (1) by 10, we get 10x = 13.4545 …..(2)
Multiplying both sides of (2) by 100, we get
1000x = 1345.4545 …….(3)
Subtracting (2) from (3), we get
990x = 1332
⇒ \(x=\frac{1332}{990}=\frac{74}{55}\)
(ii) Let x = \(2 . \overline{357}\) = 2.357357 …….(1)
Multiplying both sides of (1) by 1000, we get.
1000x = 2357.357357 ……..(2)
Subtracting (1) from (2), we get,
999x = 2355 ⇒ x = \(\frac{2355}{999}\)

Question 3.
Insert a rational number between \(\frac{5}{9}\) and \(\frac{7}{13}\), and arrange in ascending order.
Solution:

Question 4.
Insert four rational numbers between \(\frac{4}{5}\) and \(\frac{5}{6}\).
Solution:

Question 5.
Prove that the reciprocal of an irrational number is irrational.
Solution:
Let x be an irrational number
Then its reciprocal will be \(\frac{1}{x}\)
Let \(\frac{1}{x}\) is a non-zero rational number then x × \(\frac{1}{x}\) will be also irrational number as product of a non-zero rational number and irrational numbr is also irrational numbr. But
x × \(\frac{1}{x}\) = 1 which is rational number.
Our supposition is wrong.
∴ \(\frac{1}{x}\) is also an irrational number. x
Hence reciprocal of an irrational number is also an irrational number.

Question 6.
Prove that the following numbers are inrrational.

Solution:
Suppose \( \sqrt8 \) is a rational number
Let \( \sqrt8 \) = p/q where p and q are integers, q > 0 and p and q have no common factor
squaring both sides
8 = \(\frac{p^{2}}{q^{2}}\)
⇒ p² = 8 q²
∵ 8q² is divisible by 8
∴ p²2 is also divisible by 8
⇒ p is divisible by 8
Let p = 8k where k is integer.
Squaring both sides,
(p)² = (8k)²
⇒ p² = 64k²
∴ 64k² is divisible by 8
∴ p² is divisible by 8
⇒ p is divisible by 8
∴ p and q both are divisible by 8
∴ our supposition is wrong
Hence \( \sqrt8 \) is an irrational

(ii) Let \( \sqrt14 \) be a rational number and let \( \sqrt14 \) = \(\frac{p}{q}\) where p and q are integers and q ≠ 0 and
p and q have no common factor,
Squaring both sides,
14= \(\frac{p^{2}}{q^{2}}\) ⇒ p² = 14q² …(i)
∴ p² is divisible by 2
⇒ p is divisible
Let p = 2m
Substituting the value of p in (i)
(2m)² = 14q² ⇒ 4m² = 14q²
⇒ 2m² = 7q²
∴ q² is divisible by 2
⇒ q is divisible by 2
⇒ p and q have 2 as the common factor which is not possible
∴ \( \sqrt14 \) is an irrational number

(iii) \(\sqrt[3]{2}\)
suppose \(\sqrt[3]{2}\) is a rational number
Let \(\sqrt[3]{2}\) = p/q where p and q are integers, q > 0, and p and q have no common factor.
cubing both sides,
2 = \(\frac{p^{3}}{q^{3}}\)
⇒ p³ = 2q³
∵ 2q³ is divisible by 2
∴ p³ is divisible by 2
⇒ p is divisible by 2
Let p = 2k where k is an integer
cubing both sides,
(p)³ = (2k)³
⇒ p³ = 8 k³
⇒ 2 q³ = 8k³
⇒ q³ = 4k³
∵ 4k³ is divisible by 2
∴ q³ is divisible by 2
⇒ q is divisible by 2
∴ p and q both are divisible by 2
∴ our supposition is wrong
Hence \(\sqrt[3]{2}\) is an irrational number.

Question 7.
Prove that \( \sqrt3 \) is an irrational number. Hence show that \(5-\sqrt{3}\) is an irrational number.
Solution:
suppose \( \sqrt3 \) is a rational number
Let \( \sqrt3 \) = p/q where p and q are integers, q > 0 and p and q have no common factor Squaring both sides
3 = \(\frac{p^{2}}{q^{2}}\)
⇒ p² = 3 q²
∵ 3q² is divisible by 3
∴ p² is divisible by 3
⇒ p is divisible by 3
Let p = 3k where k is an integer Squaring both sides
p² = 9k²
∴ 9k² is divisible by 3
∴ p² is divisible by 3
⇒ 3q² a divisible by 3
⇒ q² is divisible by 3
⇒ q a divisible by 3
∴ p and q both are divisible by 3
∴ Our supposition is wrong .
Hence \( \sqrt3 \) is an irrational number Now in 5 – \( \sqrt3 \), 5 is a rational number and \( \sqrt3 \) is an irrational number (proved)
But difference of a rational number and an irrational number is also an irrational number
∴ (5 – \( \sqrt3 \) ) is an irrational number.
Hence proved.

Question 8.
Prove that the following numbers are irrationals

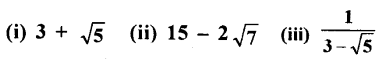
Solution:
(i) Suppose 3 + \( \sqrt5 \) is a rational number say x
Let 3 + \( \sqrt5 \) = x
\( \sqrt5 \) = x – 3
∴ x – 3 is a rational number
∴ \( \sqrt5 \) is also a rational number
Let \( \sqrt5 \) = p/q where p and q are integers, q > 0 and p and q have no common factor squaring both sides
5 = \(\frac{p^{2}}{q^{2}}\)
⇒ p² = 5 q²
∴ 5q² is divisible by 5
∴ p² is divisible by 5
⇒ p is divisible by 5
Let p = 5k, where k is an integer
squaring both sides,
P² = 25k²
⇒ 5q² = 25k²
⇒ q² = 5 k²
5k² is divisible by 5
∴ q² is divisible by 5
⇒ q is divisible by 5
∴ p and q both are divisible by 5
∴ our supposition is wrong
∴ \( \sqrt5 \) is an irrational number.
∴ 3 + \( \sqrt5 \) is also an irrational number
Hence prove.

(ii) 15 – 2\( \sqrt7 \)
suppose 15 – 2\( \sqrt7 \) is a rational number say x

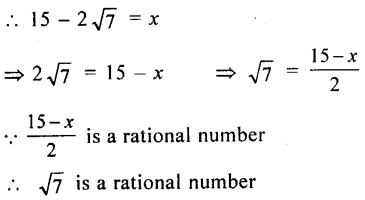
Let \( \sqrt7 \) = p/q where p and q are integers q > 0 and p and q have no common factor Squaring both sides
7 = \(\frac{p^{2}}{q^{2}}\)
⇒ p² = > 7q²
∵ 7q² is divisible by 7
⇒ p is divisible by 7
∴ p² is also divisible by 7
Let p = 7k where k is an integer Squaring both sides
p² = 49k²
⇒ 7q² = 49k²
⇒ q² = 7k²
∵ 7k² is divisible by 7
∴ q² is divisible by 7
⇒ q is divisible by 7
∴ p and q both are divisible by 7
∴ our supposition is wrong
Hence \( \sqrt7 \) is an irrational number
15 – 2 \( \sqrt7 \) is also an irrational number
Hence proved.

(iii) \(\frac{1}{3-\sqrt{5}}\)
Rationalising the denominator

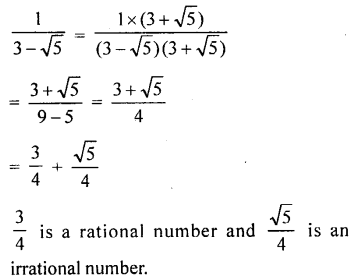
Sum of a rational and an irrational is an irrational number.
Hence proved.

Question 9.
Rationalise the denominator of the following:

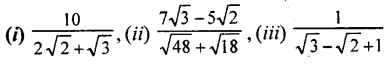
Solution:

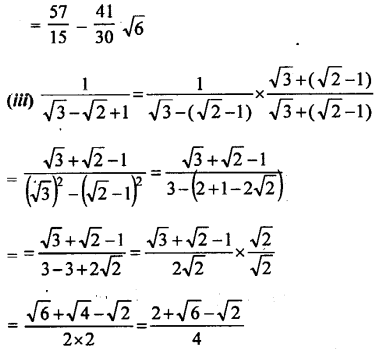
Question 10.
If p, q are rational numbers and \(p-\sqrt{15} q=\frac{2 \sqrt{3}-\sqrt{5}}{4 \sqrt{3}-3 \sqrt{5}}\) find the value of p and q.
Solution:

Question 11.
If x = \(\frac{1}{3+2 \sqrt{2}}\), then find the value of x – \(\frac{1}{x}\).
Solution:

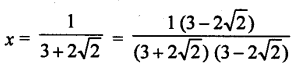
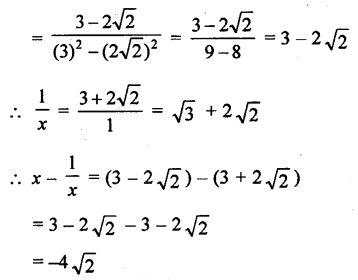
Question 12.
(i) If x = \(\frac{7+3 \sqrt{5}}{7-3 \sqrt{5}}\), find the value of

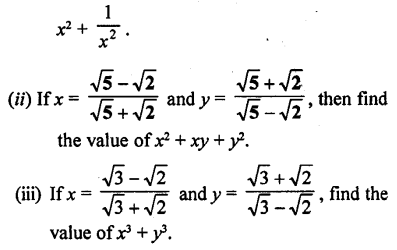
Solution:

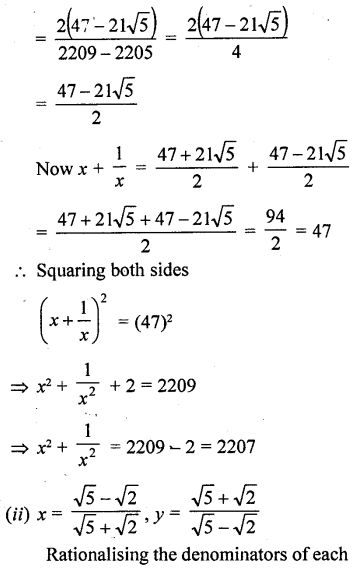
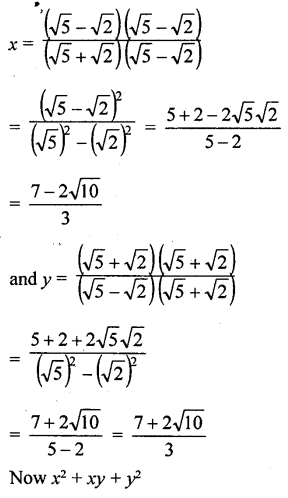
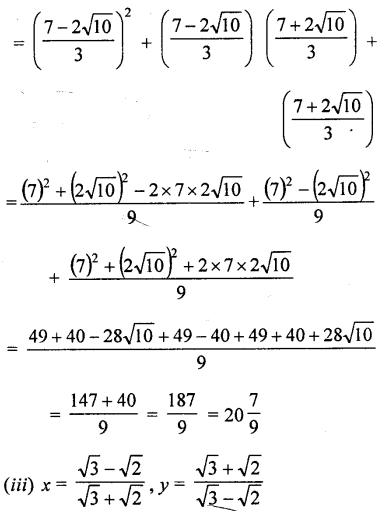
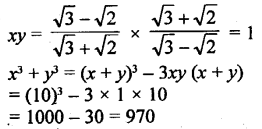
Question 13.
Write the following real numbers in descending order:

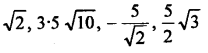
Solution:

Question 14.
Find a rational number and an irrational number between \( \sqrt3 \) and \( \sqrt5 \)?
Solution:
Consider \((\sqrt{3})^{2}\) = 3 and \( \sqrt5 \) = 5
(i) ∵ There is a rational number 4 which is perfect square of a rational number 2
(ii) There can be such more rational numbers which are perfect square.
(iii) One irrational number between \( \sqrt3 \) and \( \sqrt5 \) will be = \(\frac{1}{2}(\sqrt{3}+\sqrt{5})=\frac{\sqrt{3}+\sqrt{5}}{2}\)

Question 15.
Insert three irrational numbers between 2\( \sqrt3 \) and 2\( \sqrt5 \), and arrange in descending order.
Solution:
Consider the square

Question 16.
Give an example each of two different irrational numbers, whose
(i) sum is an irrational number.
(ii) product is an irrational number.
Solution:
(i) Let a = \( \sqrt2 \) b = \( \sqrt3 \)
Which are two irrational number
Also a + b = \( \sqrt2 \) + \( \sqrt3 \) is also irrational number
(ii) Let a = \( \sqrt2 \) b = \( \sqrt3 \)
Which are two irrational number
Also ab = \( \sqrt3 \) \( \sqrt3 \) = \( \sqrt6 \) is also irrational number

Question 17.
Give an example of two different irational numbers, a and b, where \(\frac {a}{b}\) is a rational number.
Solution:
Let a = 3\( \sqrt2 \) and b = 5\( \sqrt2 \) Which are two different irrational numbers,
But, \(\frac{a}{b}=\frac{3 \sqrt{2}}{5 \sqrt{2}}=\frac{3}{5}\) is a rational.

Question 18.
If 34.0356 is expressed in the form \(\frac {p}{q}\) where p and q are coprime integers, then what can you say about the factorisation of q ?
Solution:

which is the form of (2^m × 5ⁿ) where m and n are positive or non-negative integers.

Question 19.
In each case state whether the following numbers are rational or irrational. If they are rational and expressed in the form \(\frac {p}{q}\). where p and q are coprime integers, then what can you say about the prime factors of q ?
(i) 279.034
(ii) \(76 . \overline{17893}\)
(iii) 3.010010001
(iv) 39.546782
(v) 2.3476817681….
(vi) 59.120120012000
Solution:
(i) 279.034 is a rational number because it has terminating decimals.




(v) 2.3476817681….
It has neither terminating decimals nor repeated
∴ It is an irrational numbers
(vi) 59.120120012000
It has neither terminating decimals nor repeated
∴ It is an irrational number

ML Aggarwal Class 9 Solutions for ICSE Maths