ML Aggarwal Class 10 Solutions Matrices Chapter Test
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Matrices Chapter Test.
ML Aggarwal SolutionsICSE SolutionsSelina ICSE Solutions
Question 1.
Find the values of a and below
\(\begin{bmatrix} a+3 & { b }^{ 2 }+2 \\ 0 & -6 \end{bmatrix}=\begin{bmatrix} 2a+1 & 3b \\ 0 & { b }^{ 2 }-5b \end{bmatrix}\)
Solution:
\(\begin{bmatrix} a+3 & { b }^{ 2 }+2 \\ 0 & -6 \end{bmatrix}=\begin{bmatrix} 2a+1 & 3b \\ 0 & { b }^{ 2 }-5b \end{bmatrix}\)
comparing the corresponding elements
a + 3 = 2a + 1
=> 2a – a =3 – 1
=> a = 2
b² + 2 = 3b
=>b² – 3b + 2 = 0
=> b² – b – 2b + 2 = 0
=> b (b – 1) – 2 (b – 1) = 0
=> (b – 1) (b – 2) = 0.
Either b – 1 = 0, then b = 1 or b – 2 = 0,
then b = 2
Hence a = 2, 5 = 2 or 1 Ans.
Question 2.
Find a, b, c and d if \(3\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 4 & a+b \\ c+d & 3 \end{bmatrix}+\begin{bmatrix} a & 6 \\ -1 & 2d \end{bmatrix}\)
Solution:
Given
\(3\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 4 & a+b \\ c+d & 3 \end{bmatrix}+\begin{bmatrix} a & 6 \\ -1 & 2d \end{bmatrix}\)

Question 3.
Find X if Y = \(\begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix} \) and 2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \)
Solution:
Given
2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \)
=> 2X = 2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \) – Y
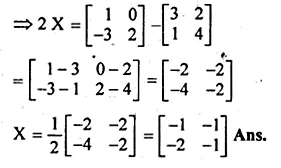
Question 4.
Determine the matrices A and B when
A + 2B = \(\begin{bmatrix} 1 & 2 \\ 6 & -3 \end{bmatrix} \) and 2A – B = \(\begin{bmatrix} 2 & -1 \\ 2 & -1 \end{bmatrix} \)
Solution:
A + 2B = \(\begin{bmatrix} 1 & 2 \\ 6 & -3 \end{bmatrix} \)…..(i)
2A – B = \(\begin{bmatrix} 2 & -1 \\ 2 & -1 \end{bmatrix} \)…….(ii)
Multiplying (i) by 1 and (ii) by 2

Question 5.
(i) Find the matrix B if A = \(\begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} \) and A² = A + 2B
(ii) If A = \(\begin{bmatrix} 1 & 2 \\ -3 & 4 \end{bmatrix} \), B = \(\begin{bmatrix} 0 & 1 \\ -2 & 5 \end{bmatrix} \)
and C = \(\begin{bmatrix} -2 & 0 \\ -1 & 1 \end{bmatrix} \) find A(4B – 3C)
Solution:
A = \(\begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} \)
let B = \(\begin{bmatrix} a & b \\ c & d \end{bmatrix} \)

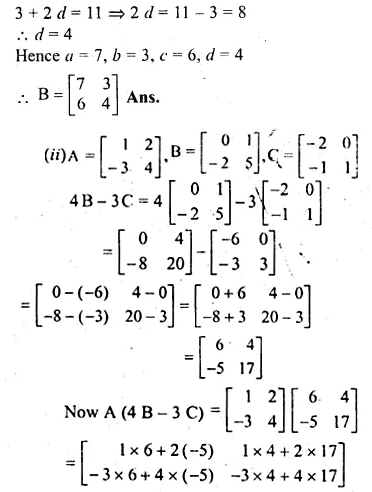
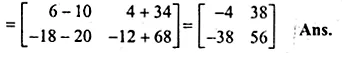
Question 6.
If A = \(\begin{bmatrix} 1 & 4 \\ 1 & 0 \end{bmatrix} \), B = \(\begin{bmatrix} 2 & 1 \\ 3 & -1 \end{bmatrix} \) and C = \(\begin{bmatrix} 2 & 3 \\ 0 & 5 \end{bmatrix} \) compute (AB)C = (CB)A ?
Solution:
Given
A = \(\begin{bmatrix} 1 & 4 \\ 1 & 0 \end{bmatrix} \),
B = \(\begin{bmatrix} 2 & 1 \\ 3 & -1 \end{bmatrix} \) and
C = \(\begin{bmatrix} 2 & 3 \\ 0 & 5 \end{bmatrix} \)
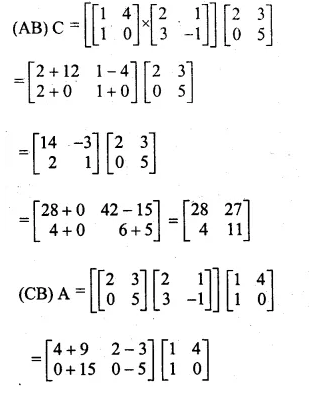

Question 7.
If A = \(\begin{bmatrix} 3 & 2 \\ 0 & 5 \end{bmatrix} \) and B = \(\begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix} \) find the each of the following and state it they are equal:
(i) (A + B)(A – B)
(ii)A² – B²
Solution:
Given
A = \(\begin{bmatrix} 3 & 2 \\ 0 & 5 \end{bmatrix} \) and
B = \(\begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix} \)
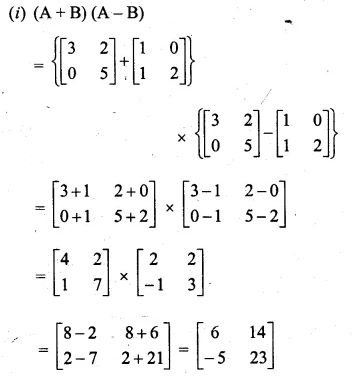
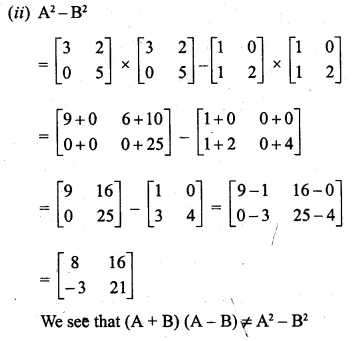
Question 8.
If A = \(\begin{bmatrix} 3 & -5 \\ -4 & 2 \end{bmatrix} \) find A² – 5A – 14I
Where I is unit matrix of order 2 x 2
Solution:
Given
A = \(\begin{bmatrix} 3 & -5 \\ -4 & 2 \end{bmatrix} \)
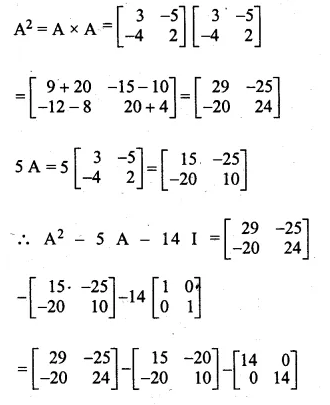
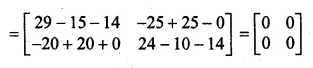
Question 9.
If A = \(\begin{bmatrix} 3 & 3 \\ p & q \end{bmatrix} \) and A² = 0 find p and q
Solution:
Given
A = \(\begin{bmatrix} 3 & 3 \\ p & q \end{bmatrix} \)

Question 10.
If A = \(\begin{bmatrix} \frac { 3 }{ 5 } & \frac { 2 }{ 5 } \\ x & y \end{bmatrix} \) and A² = I, find x,y
Solution:
Given
A = \(\begin{bmatrix} \frac { 3 }{ 5 } & \frac { 2 }{ 5 } \\ x & y \end{bmatrix} \)
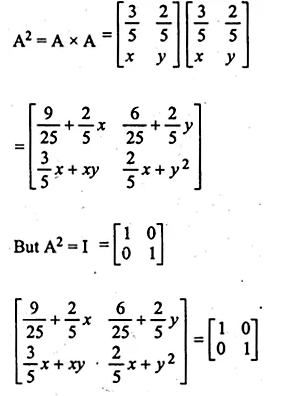
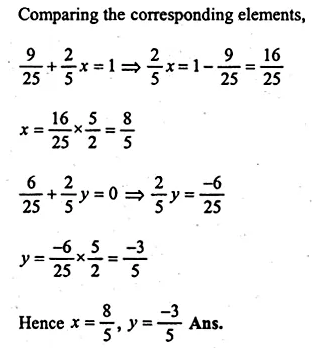
Question 11.
If \(\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \) find a,b,c and d
Solution:
Given
\(\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \)

Question 12.
Find a and b if
\(\begin{bmatrix} a-b & b-4 \\ b+4 & a-2 \end{bmatrix}\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}=\begin{bmatrix} -2 & -2 \\ 14 & 0 \end{bmatrix} \)
Solution:
Given
\(\begin{bmatrix} a-b & b-4 \\ b+4 & a-2 \end{bmatrix}\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}=\begin{bmatrix} -2 & -2 \\ 14 & 0 \end{bmatrix} \)

Question 13.
If A = \(\begin{bmatrix} { sec60 }^{ o } & { cos90 }^{ o } \\ { -3tan45 }^{ o } & { sin90 }^{ o } \end{bmatrix} \) and B = \(\begin{bmatrix} 0 & { cos45 }^{ o } \\ -2 & { 3sin90 }^{ o } \end{bmatrix} \)
Find (i) 2A – 3B (ii) A² (iii) BA
Solution:
Given
A = \(\begin{bmatrix} { sec60 }^{ o } & { cos90 }^{ o } \\ { -3tan45 }^{ o } & { sin90 }^{ o } \end{bmatrix} \) and
B = \(\begin{bmatrix} 0 & { cos45 }^{ o } \\ -2 & { 3sin90 }^{ o } \end{bmatrix} \)
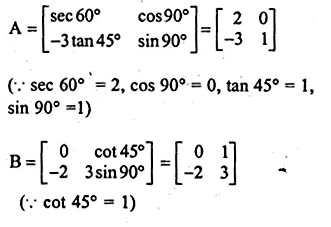

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Matrices Chapter Test are helpful to complete your math homework.
If you have any doubts, please comment below. APlusTopper try to provide online math tutoring for you.
