ML Aggarwal Class 10 Solutions Quadratic Equations in One Variable Chapter Test
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Quadratic Equations in One Variable Chapter Test
ML Aggarwal SolutionsICSE SolutionsSelina ICSE Solutions
Solve the following equations (1 to 4) by factorisation :
Question 1.
(i) x² + 6x – 16 = 0
(ii) 3x² + 11x + 10 = 0
Solution:
x² + 6x – 16 = 0
=> x² + 8x – 2x – 16 = 0
x (x + 8) – 2 (x + 8) = 0
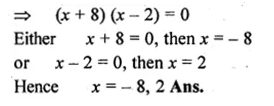
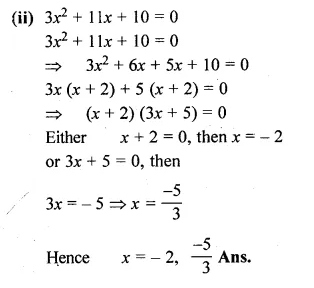
Question 2.
(i) 2x² + ax – a² = 0
(ii) √3x² + 10x + 7√3 = 0
Solution:
(i) 2x² + ax – a² = 0
=> 2x² + 2ax – ax – a² = 0
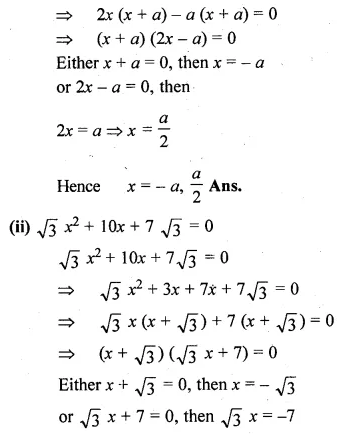
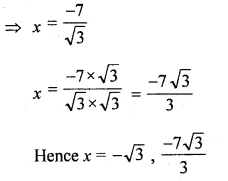
Question 3.
(i) x(x + 1) + (x + 2)(x + 3) = 42
(ii) \(\frac { 6 }{ x } -\frac { 2 }{ x-1 } =\frac { 1 }{ x-2 } \)
Solution:
(i) x(x + 1) + (x + 2)(x + 3) = 42
2x² + 6x + 6 – 42 = 0
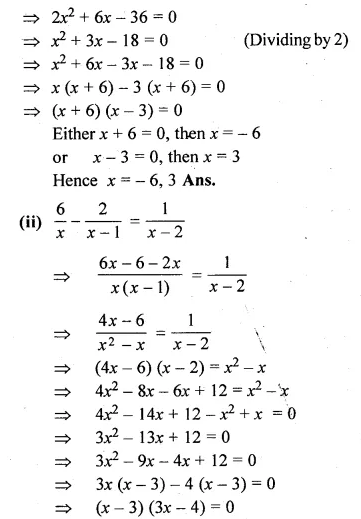
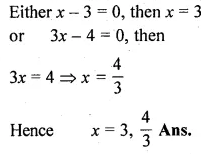
Question 4.
(i)\(\sqrt { x+15 } =x+3 \)
(ii)\(\sqrt { { 3x }^{ 2 }-2x-1 } =2x-2\)
Solution:
(i)\(\sqrt { x+15 } =x+3 \)
Squaring on both sides
x + 15 = (x + 3)²
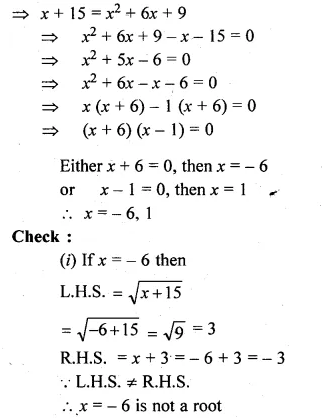
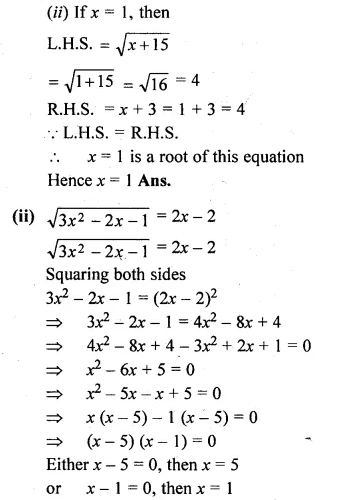

Solve the following equations (5 to 8) by using formula :
Question 5.
(i) 2x² – 3x – 1 = 0
(ii) \(x\left( 3x+\frac { 1 }{ 2 } \right) =6\)
Solution:
(i) 2x² – 3x – 1 = 0
Here a = 2, b = – 3, c = – 1
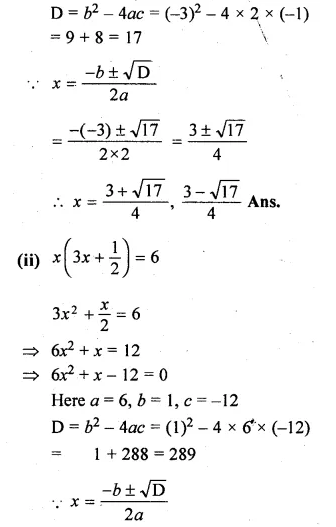
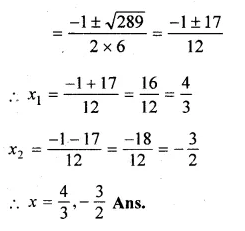
Question 6.
(i) \(\frac { 2x+5 }{ 3x+4 } =\frac { x+1 }{ x+3 } \)
(ii) \(\frac { 2 }{ x+2 } -\frac { 1 }{ x+1 } =\frac { 4 }{ x+4 } -\frac { 3 }{ x+3 } \)
Solution:
(i) \(\frac { 2x+5 }{ 3x+4 } =\frac { x+1 }{ x+3 } \)
(2x + 5)(x + 3) = (x + 1)(3x + 4)
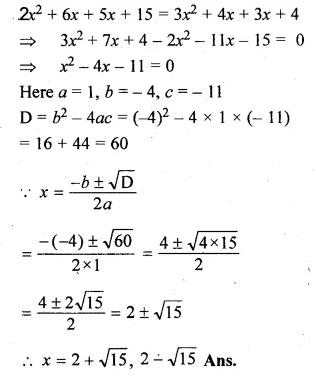
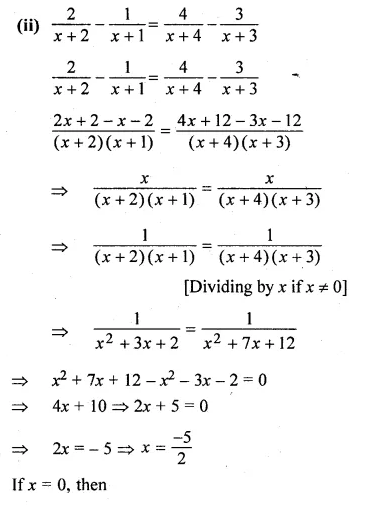
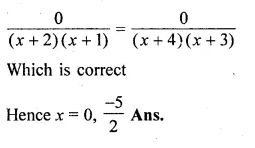
Question 7.
(i) \(\frac { 3x-4 }{ 7 } +\frac { 7 }{ 3x-4 } =\frac { 5 }{ 2 } ,x\neq \frac { 4 }{ 3 } \)
(ii) \(\frac { 4 }{ x } -3=\frac { 5 }{ 2x+3 } ,x\neq 0,-\frac { 3 }{ 2 } \)
Solution:
(i) \(\frac { 3x-4 }{ 7 } +\frac { 7 }{ 3x-4 } =\frac { 5 }{ 2 } ,x\neq \frac { 4 }{ 3 } \)
let \(\frac { 3x-4 }{ 7 } \) = y,then
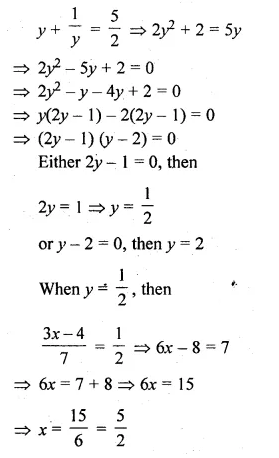
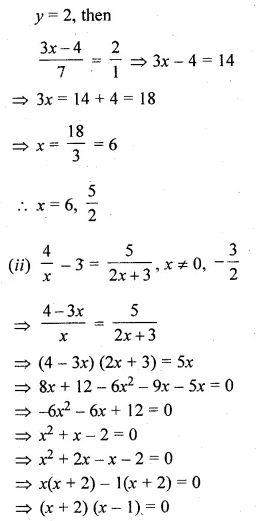
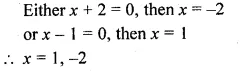
Question 8.
(i)x² + (4 – 3a)x – 12a = 0
(ii)10ax² – 6x + 15ax – 9 = 0,a≠0
Solution:
(i)x² + (4 – 3a)x – 12a = 0
Here a = 1,b = 4 – 3a,c = – 12a
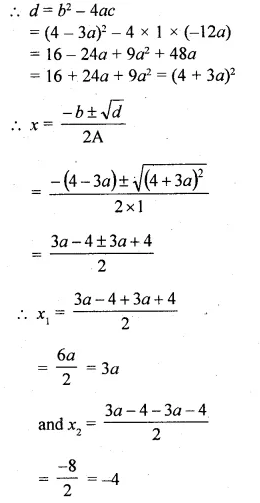
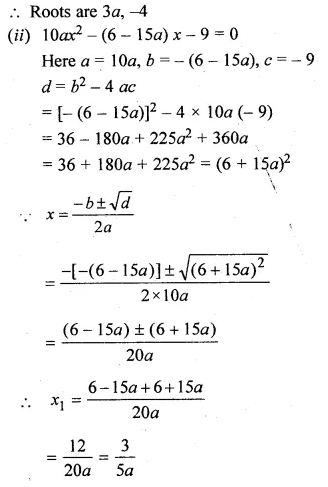
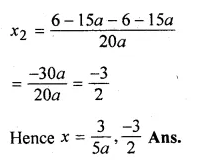
Question 9.
Solve for x using the quadratic formula. Write your answer correct to two significant figures: (x – 1)² – 3x + 4 = 0. (2014)
Solution:
(x – 1)² – 3x + 4 = 0
x² + 1 – 2x – 3x + 4 = 0
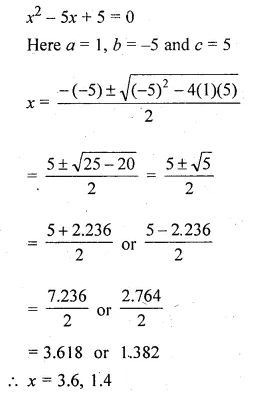
Question 10.
Discuss the nature of the roots of the following equations:
(i) 3x² – 7x + 8 = 0
(ii) x² – \(\\ \frac { 1 }{ 2 } x\) – 4 = 0
(iii) 5x² – 6√5x + 9 = 0
(iv) √3x² – 2x – √3 = 0
Solution:
(i) 3x² – 7x + 8 = 0
Here a = 3, b = – 7,c = 8
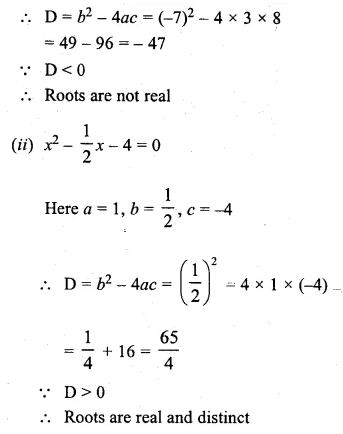
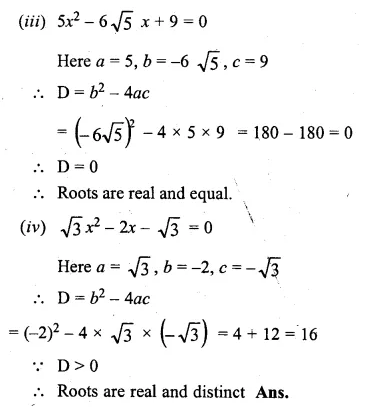
Question 11.
Find the values of k so that the quadratic equation (4 – k) x² + 2 (k + 2) x + (8k + 1) = 0 has equal roots.
Solution:
(4 – k) x² + 2 (k + 2) x + (8k + 1) = 0
Here a = (4 – k), b = 2 (k + 2), c = 8k + 1
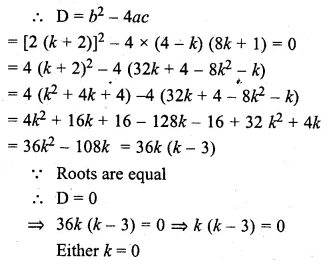
or k – 3 = 0, then k= 3
k = 0, 3 Ans.
Question 12.
Find the values of m so that the quadratic equation 3x² – 5x – 2m = 0 has two distinct real roots.
Solution:
3x² – 5x – 2m = 0
Here a = 3, b = – 5, c = – 2m
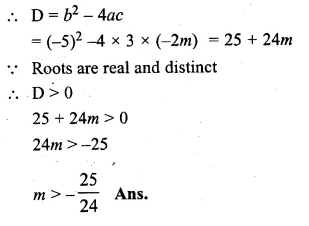
Question 13.
Find the value(s) of k for which each of the following quadratic equation has equal roots:
(i)3kx² = 4(kx – 1)
(ii)(k + 4)x² + (k + 1)x + 1 =0
Also, find the roots for that value (s) of k in each case.
Solution:
(i)3kx² = 4(kx – 1)
=> 3kx² = 4kx – 4
=> 3kx² – 4kx + 4 = 0
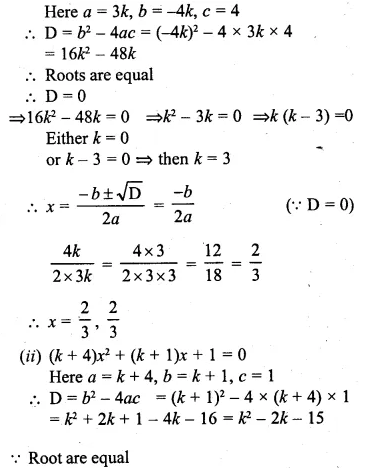
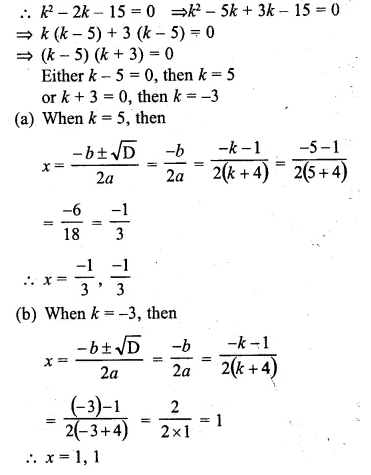
Question 14.
Find two natural numbers which differ by 3 and whose squares have the sum 117.
Solution:
Let first natural number = x
then second natural number = x + 3
According to the condition :
x² + (x + 3)² = 117
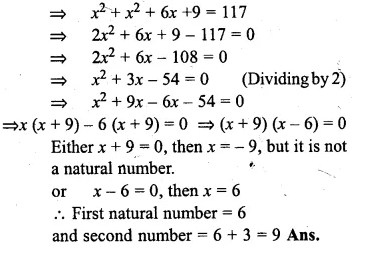
Question 15.
Divide 16 into two parts such that the twice the square of the larger part exceeds the square of the smaller part by 164.
Solution:
Let larger part = x
then smaller part = 16 – x
(∵ sum = 16)
According to the condition
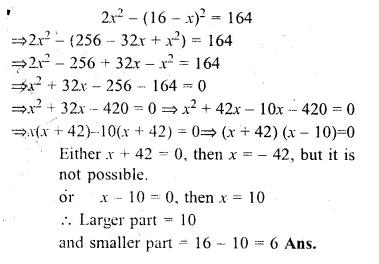
Question 16.
Two natural numbers are in the ratio 3 : 4. Find the numbers if the difference between their squares is 175.
Solution:
Ratio in two natural numbers = 3 : 4
Let the numbers be 3x and 4x
According to the condition,
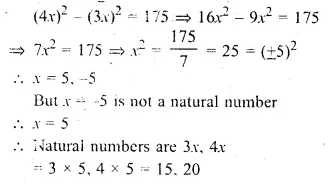
Question 17.
Two squares have sides A cm and (x + 4) cm. The sum of their areas is 656 sq. cm.Express this as an algebraic equation and solve it to find the sides of the squares.
Solution:
Side of first square = x cm .
and side of second square = (x + 4) cm
Now according to the condition,
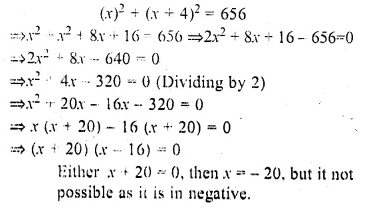
or x – 16 = 0 then x = 16
Side of first square = 16 cm
and side of second square = 16 + 4 – 4
= 20 cm Ans.
Question 18.
The length of a rectangular garden is 12 m more than its breadth. The numerical value of its area is equal to 4 times the numerical value of its perimeter. Find the dimensions of the garden.
Solution:
Let breadth = x m
then length = (x + 12) m
Area = l × b = x (x + 12) m²
and perimeter = 2 (l + b)
= 2(x + 12 + x) = 2 (2x + 12) m
According to the condition.
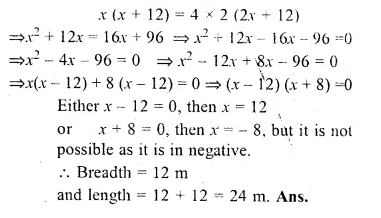
Question 19.
A farmer wishes to grow a 100 m² rectangular vegetable garden. Since he has with him only 30 m barbed wire, he fences three sides of the rectangular garden letting compound wall of his house act as the fourth side fence. Find the dimensions of his garden.
Solution:
Area of rectangular garden = 100 cm²
Length of barbed wire = 30 m
Let the length of side opposite to wall = x

Question 20.
The hypotenuse of a right angled triangle is 1 m less than twice the shortest side. If the third side is 1 m more than the shortest side, find the sides of the triangle.
Solution:
Let the length of shortest side = x m
Length of hypotenuse = 2x – 1
and third side = x + 1
Now according to the condition,

Question 21.
A wire ; 112 cm long is bent to form a right angled triangle. If the hypotenuse is 50 cm long, find the area of the triangle.
Solution:
Perimeter of a right angled triangle = 112 cm
Hypotenuse = 50 cm
∴ Sum of other two sides = 112 – 50 = 62 cm
Let the length of first side = x
and length of other side = 62 – x

Question 22.
Car A travels x km for every litre of petrol, while car B travels (x + 5) km for every litre of petrol.
(i) Write down the number of litres of petrol used by car A and car B in covering a distance of 400 km.
(ii) If car A uses 4 litres of petrol more than car B in covering 400 km. write down an equation, in A and solve it to determine the number of litres of petrol used by car B for the journey.
Solution:
Distance travelled by car A in one litre = x km
and distance travelled by car B in one litre = (x + 5) km
(i) Consumption of car A in covering 400 km

Question 23.
The speed of a boat in still water is 11 km/ hr. It can go 12 km up-stream and return downstream to the original point in 2 hours 45 minutes. Find the speed of the stream
Solution:
Speed of boat in still water =11 km/hr
Let the speed of stream = x km/hr.
Distance covered = 12 km.
Time taken = 2 hours 45 minutes .
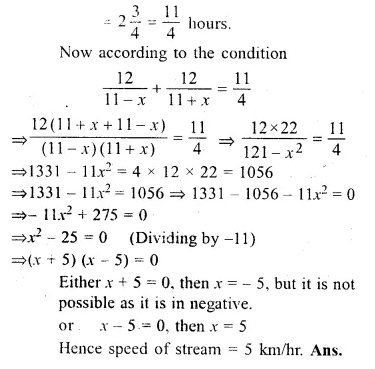
Question 24.
By selling an article for Rs. 21, a trader loses as much percent as the cost price of the article. Find the cost price.
Solution:
S.R of an article = Rs. 21
Let cost price = Rs. x
Then loss = x%
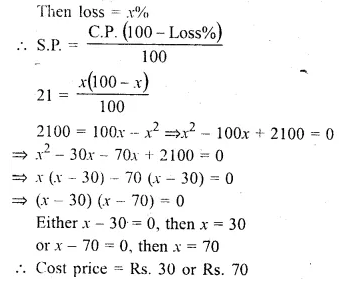
Question 25.
A man spent Rs. 2800 on buying a number of plants priced at Rs x each. Because of the number involved, the supplier reduced the price of each plant by Rupee 1.The man finally paid Rs. 2730 and received 10 more plants. Find x.
Solution:
Amount spent = Rs. 2800
Price of each plant = Rs. x
Reduced price = Rs. (x – 1)

Question 26.
Forty years hence, Mr. Pratap’s age will be the square of what it was 32 years ago. Find his present age.
Solution:
Let Partap’s present age = x years
40 years hence his age = x + 40
and 32 years ago his age = x – 32
According to the condition
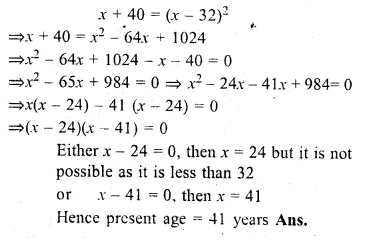
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Quadratic Equations in One Variable Chapter Test are helpful to complete your math homework.
If you have any doubts, please comment below. APlusTopper try to provide online math tutoring for you.
