Solving Trigonometric Equations
Important points to be taken in case of while solving trigonometrical equations
- Check the validity of the given equation, e.g. 2 sin θ – cos θ = 4 can never be true for any θ as the value (2 sin θ – cos θ) can never exceeds √(22 + (−1)2) = √5. So there is no solution of this equation.
- Equation involving sec θ or tan θ can never have a solution of the form, (2n + 1)π/2.
Similarly, equations involving cosec θ or cot θ can never have a solution of the form θ = nπ. The corresponding functions are undefined at these values of θ. - If while solving an equation we have to square it, then the roots found after squaring must be checked whether they satisfy the original equation or not, e.g. let x = 3. Squaring, we get x2 = 9
∴ x = 3 and −3 but x = −3 does not satisfy the original equation x = 3. - Do not cancel common factors involving the unknown angle on L.H.S. and R.H.S. because it may delete some solutions. In the equation sin θ(2 cos θ – 1) = sin θ cos2 θ if we cancel sin θ on both sides we get cos2 θ – 2 cos θ + 1 = 0 ⇒ (cos θ – 1)2 = 0 ⇒ cos θ = 1 ⇒ θ = 2nπ. But θ = nπ also satisfies the equation because it makes sin θ = 0. So, the complete solution is θ = nπ, n ∈ Z.
- Any value of x which makes both R.H.S. and L.H.S. equal will be a root but the value of x for which ∞ = ∞ will not be a solution as it is an indeterminate form.
Hence, cos x ≠ 0 for those equations which involve tan x and sec x whereas sin x ≠ 0 for those which involve cot x and cosec x.
Also exponential function is always +ve and loga x is defined if x > 0, x ≠ 0 and a > 0, a ≠ 0 √f(x) = +ve always and not ± i.e. √(tan2 x) = tan x and not ± tan x. - Denominator terms of the equation if present should never become zero at any stage while solving for any value of q contained in the answer.
- Sometimes the equation has some limitations also e.g., cot2 θ + cosec2 θ = 1 can be true only if cot2 θ = 0 and cosec2 θ = 1 simultaneously as cosec2 θ ≥ 1. Hence the solution is θ = (2n + 1)π/2.
- If xy = xz then x(y – z) = 0 ⇒ either x = 0 or y = z or both. But y/x = z/x ⇒ y = z only and not x = 0, as it will make ∞ = ∞. Similarly if ay = az, then it will also imply y = z only as a ≠ 0 being a constant.
Similarly x + y = x + z ⇒ y = z and x – y = x – z ⇒ y = z. Here we do not take x = 0 as in the above because x is an additive factor and not multiplicative factor. - Student are advised to check whether all the roots obtained by them, satisfy the equation and lie in the domain of the variable of the given equation.
Trigonometric Equations involving Powers:
When the trig function has a power, it will have to be solved by extracting square roots or factoring.
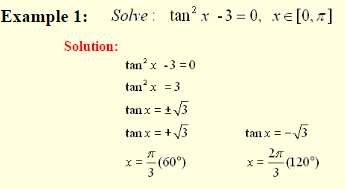
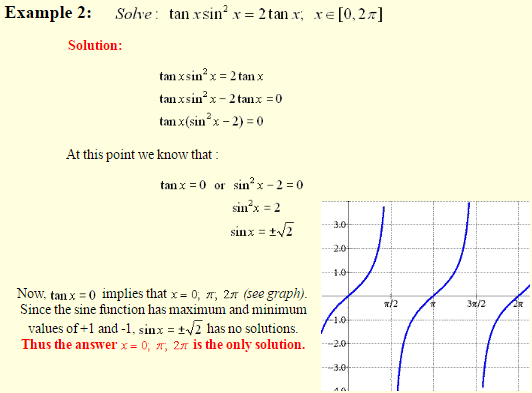

Solving Quadratic Equations:
Remember to first solve for the trig function and then solve for the angle value.
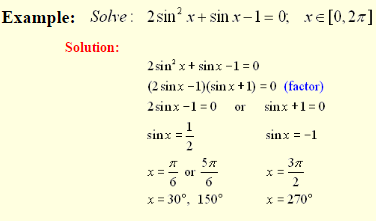

Using Identities in Equation Solving:
If there is more than one trig function in the equation,
identities are needed to reduce the equation to a single function for solving.

