Mean Proportional in a Right Triangle
“Mean Proportional” may also be referred to as a “Geometric Mean”.
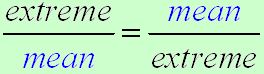Remember the rule for working with proportions: the product of the means equals the product of the extremes.
Definition:
The mean proportional of two positive numbers a and b is the positive number x such that \(\frac { a }{ x } =\frac { x }{ b }\). When solving \(x=\sqrt { a.b }\).
Notice that the x value appears TWICE in the “means” positions.
Theorem:
The altitude to the hypotenuse of a right triangle forms two triangles that are similar to each other and to the original triangle.
Since these triangles are similar, we can establish proportions relating the corresponding sides. Two valuable theorems can be formed using these proportions.
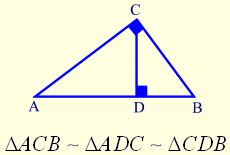Theorem:
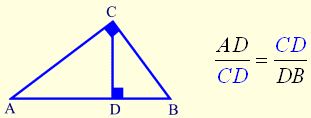
The altitude to the hypotenuse of a right triangle is the mean proportional between the segments into which it divides the hypotenuse.
Altitude Rule:
\(\frac { part\quad of\quad hyp }{ altitude } =\frac { altitude }{ other\quad part\quad of\quad hyp }\)
Theorem:
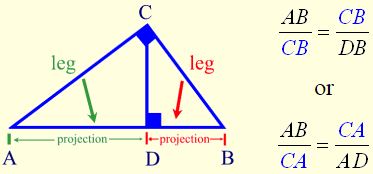
Each leg of a right triangle is the mean proportional between the hypotenuse and the projection of the leg on the hypotenuse.
Leg Rule:
\(\frac { hypotenuse }{ leg } =\frac { leg }{ projection } \)
Examples:
