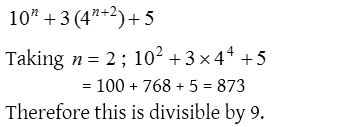What is Mathematical Induction in Discrete Mathematics?

What is Mathematical Induction in Discrete Mathematics?

First principle of Mathematical induction

The proof of proposition by mathematical induction consists of the following three steps :

Step I : (Verification step) : Actual verification of the proposition for the starting value “i”.

Step II : (Induction step) : Assuming the proposition to be true for “k”, k ≥ i and proving that it is true for the value (k + 1) which is next higher integer.

Step III : (Generalization step) : To combine the above two steps. Let p(n) be a statement involving the natural number n such that

1. p(1) is true i.e. p(n) is true for n = 1.
2. p(m + 1) is true, whenever p(m) is true i.e. p(m) is true ⇒ p(m + 1) is true.

Then p(n) is true for all natural numbers n.

Second principle of Mathematical induction

The proof of proposition by mathematical induction consists of following steps :

Step I : (Verification step) : Actual verification of the proposition for the starting value i and (i + 1).

Step II : (Induction step) : Assuming the proposition to be true for k – 1 and k and then proving that it is true for the value k + 1; k ≥ i + 1.

Step III : (Generalization step) : Combining the above two steps. Let p(n) be a statement involving the natural number n such that

1. p(1) is true i.e. p(n) is true for n = 1 and
2. p(m + 1) is true, whenever p(n) is true for all n, where i ≤  n ≤ m.

Then p(n) is true for all natural numbers.
For a ≠ b, The expression is divisible by
(a) a + b, if n is even.
(b) a – b, if n is odd or even.

Divisibility problems

To show that an expression is divisible by an integer

1. If a, p, n, r are positive integers, then first of all we write a^pn+r = a^pn . a^r = (a^p)ⁿ . a^r.
2. If we have to show that the given expression is divisible by c.

Then express, a^p = [1 + (a^p – 1)], if some power of (a^p – 1) has c as a factor. a^p = [2 + (a^p – 2)], if some power of (a^p – 2) has c as a factor.
a^p = [k + (a^p – k)], if some power of (a^p – k) has c as a factor.

Mathematical Induction Problems with Solutions

1. For all positive integral values of n, 3²ⁿ – 2n + 1 is divisible by
(a)  2
(b)  4
(c)  8
(d)  12
Solution:
Putting n = 2 in 3²ⁿ – 2n + 1 then, 3²⁽²⁾ – 2×2 + 1 = 81 – 4 + 1 = 78, which is divisible by 2.

2. If n ∈ N, then x^{2n – 1} + y^{2n – 1} is divisible by
(a)  x +y
(b)  x – y
(c)  x² + y²
(d)  x² + xy
Solution:
x^{2n – 1} + y^{2n – 1} is always contain equal odd power. So it is always divisible by x + y.

3. If n ∈ N, then 7²ⁿ + 2^{3n – 3} . 3^{n – 1} is always divisible by
(a)  25
(b)  35
(c)  45
(d)  None of these
Solution:

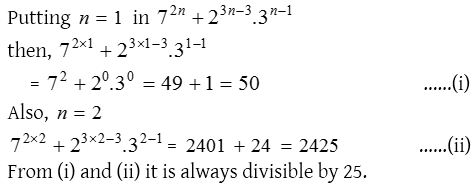
4. If n ∈ N, then 11^{n + 2} + 12^{2n + 1} is divisible by
(a)  113
(b)  123
(c)  133
(d)  None of these
Solution:

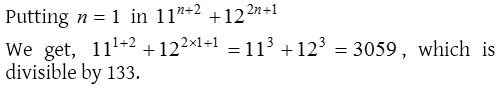
5. The remainder when 5⁹⁹ is divided by 13 is
(a)  6
(b)  8
(c)  9
(d)  10
Solution:

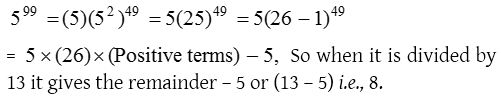
6. When 2³⁰¹ is divided by 5, the least positive remainder is
(a)  4
(b)  8
(c)  2
(d)  6
Solution:

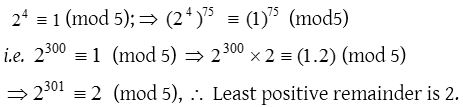
7. For a positive integer n,

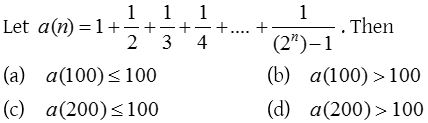
Solution:

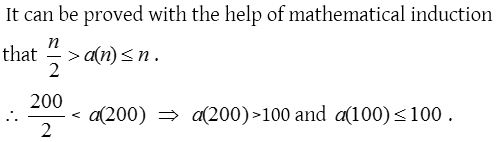
8. 10ⁿ + 3(4^{n + 2}) + 5 is divisible by (n ∈ N)
(a)  7
(b)  5
(c)  9
(d)  17
(e)  13
Solution: