Math Labs with Activity – Surface Area of a Sphere Formula
OBJECTIVE
To demonstrate a method to derive a formula to find the surface area of a sphere
Materials Required
- A hollow spherical ball of known radius
- A cylinder having its height equal to twice the radius of the spherical ball and base radius equal to the radius of the spherical ball
- A knife
- A long nylon thread of uniform thickness
Theory
The curved surface area of a cylinder having the base radius r and height h is given by 2πrh.
If the height is taken to be 2r then the curved surface area of the cylinder becomes 4πr².
It can be shown that this area is equal to the area of a sphere of radius r.
Procedure
Step 1: Take a hollow spherical ball of radius r and cut it into two hemispheres. Wind a nylon thread closely around one of the hemispheres so that the thread completely covers its curved surface as shown in Figure 39.1.
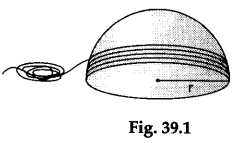
Step 2: Take a right-circular cylinder having its height equal to 2r and its base radius equal to r. Wind a similar nylon thread closely around it so that the thread completely covers its curved surface, as shown in Figure 39.2.
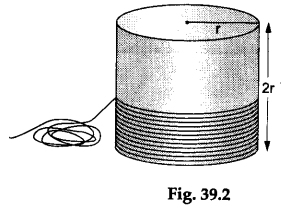
Step 3: Measure the lengths of the two threads.
Observations and Calculations
We observe that the length of the thread wound over the curved surface of the cylinder is twice the length of the thread wound over the curved surface of the hemisphere.
Since the thickness of the thread is uniform, the surface areas are approximately proportional to the lengths of the threads.
∴ curved surface area of the cylinder = 2 x curved surface area of the hemisphere = surface area of the complete sphere.
The curved surface area of the cylinder = 2πrh [∴ h=2r]
= 2πr . 2r = 4πr².
∴ surface area of the sphere = 4πr².
Result
The surface area of a sphere of radius r is given by 4πr².
Math Labs with ActivityMath LabsScience Practical SkillsScience Labs
