A Plus Topper

Improve your Grades

Math Labs with Activity - Ratio of the Areas of two Similar Triangle

by

Math Labs with Activity – Ratio of the Areas of two Similar Triangle

OBJECTIVE

To verify that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides

Materials Required

  1. A piece of cardboard
  2. A sheet of white paper
  3. A geometry box
  4. A tube of glue

Theory
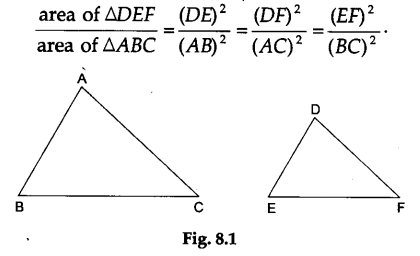
If two triangles ABC and DEF are similar then area of ΔDEF
Math Labs with Activity - Ratio of the Areas of two Similar Triangle 1

Procedure
Step 1: Paste the white sheet on the cardboard.
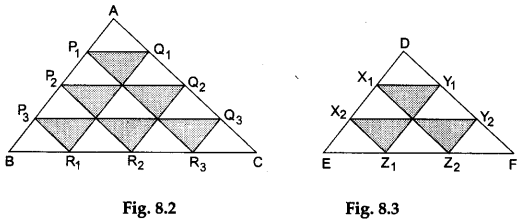
Step 2: Draw a ΔABC on the paper. Now, divide the side AB into four equal parts and label these points P1, P2 and P3 as shown in Figure 8.2. Similarly, divide the side AC into four equal parts and label these points Q1, Q2 and Q3 as shown in Figure 8.2. Also, divide the side BC into equal parts and label these points R1, R2 and R3 as shown in Figure 8.2.
Step 3: Join these points to form the line segments P1Q1, P2Q2 and P3Q3 parallel to the side BC, the line segments Q1R1, Q2R2 and Q3R3 parallel to the side AB, and also the line segments P3R1, P2R2 and P1R3 parallel to the side AC. Thus, the ΔABC is divided into 16 smaller triangles (see Figure 8.2).
Step 4: Draw another triangle DEF having sides DE = ¾ AB, DF = ¾ AC and EF = ¾ BC. Then, clearly the ΔDEF will be similar to the ΔABC.
Step 5: Divide the side DE into three equal parts and label these points X1 and X2 as shown in Figure 8.3.
Divide the side DF into three equal parts and label these points Y1 and Y2 as shown in Figure 8.3.
Also, divide the side EE into three equal parts and label these points Z1 and Z2 as shown in Figure 8.3.
Step 6: Join these points to form the line segments X1Y1 and X2Y2 parallel to the side EE, the line segments Y1Z1 and Y2Z2 parallel to the side DE, and also the line segments X1Z2 and X2Z1 parallel to the side DF. Thus, the ΔDEE is divided into 9 smaller triangles (see Figure 8.3).
Math Labs with Activity - Ratio of the Areas of two Similar Triangle 2

Observations

  1. ΔABC and ΔDEF are similar to each other.
  2. ΔABC is divided into 16 smaller triangles, all congruent to each other. Therefore, all these 16 triangles are equal in area.
  3. ΔDEF is divided into 9 smaller triangles, all congruent to each other. Therefore, all these 9 triangles are equal in area.
  4. Each small triangle within the ΔABC is congruent to each small triangle within the ΔDEF. Therefore, all these 25 triangles are equal in area (say, equal to M).

Calculations
Math Labs with Activity - Ratio of the Areas of two Similar Triangle 3

Result
It is verified that the ratio of the areas of two similar triangles is equal to the ratio of the squares of the corresponding sides.

Remarks:
The above result can also be proved for

  1. other pairs of corresponding sides of the two triangles.
  2. other triangles by dividing each side of a triangle into 3, 4,5 or 6 or even more parts and forming small triangles, and then taking a part of this triangle as a similar triangle.

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs