Math Labs with Activity - Pythagoras' theorem (Method 5)

Math Labs with Activity – Pythagoras theorem (Method 5)

OBJECTIVE

To verify Pythagoras’ theorem (Method 5)

Materials Required

1. A piece of cardboard
2. Two sheets of white paper
3. A pair of scissors
4. A geometry box
5. A tube of glue

Theory
Pythagoras’ theorem: In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Procedure
Step 1: Paste a sheet of white paper on the cardboard.
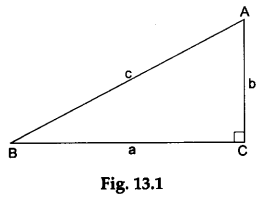
On this paper, draw a right-angled triangle ABC, right angled at C. Let the lengths of the sides AB, BC and CA be c, a and b units respectively (see Figure 13.1).

Step 2: Calculate (a-b). On the other paper, draw a square with each side measuring (a-b) units. Also, draw a square with each side measuring c units.
Step 3: Make four exact copies of the ΔABC on the second paper.
Step 4: Cut the two squares and the four triangles from the second paper.
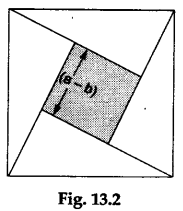
Step 5: Arrange the square with each side measuring (a-b) units, along with the four triangles, as shown in Figure 13.2, Place this arrangement over the square of side c units.

Observations
We observe that the square of side (a-b) units, together with the four triangles, completely covers the square of side c units when arranged as shown in Figure 13.2.

Calculations
Area of the square with each side measuring c units = area of the square with each side measuring (a-b) units + 4 (area of the ΔABC)
i.e., c² = (a – b)² + 4 (½ x a x b)
=> c² = (a² + b² – 2ab) + 2ab
=> c² = a² + b².
In other words, the square of the hypotenuse of the right-angled ΔABC is equal to the sum of the squares of the other two sides.

Result
Pythagoras’ theorem is verified.

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs