Math Labs with Activity - Paper Cutting and Folding Method

Math Labs with Activity – Paper Cutting and Folding Method

OBJECTIVE

To verify by the method of paper cutting and folding that

1. the angle in a semicircle is a right angle
2. the angle in a minor segment is an obtuse angle
3. the angle in a major segment is an acute angle

Materials Required

1. Three sheets of white paper
2. A tracing paper
3. A geometry box

Procedure
To verify that the angle in a semicircle is a right angle.
Step 1: Take a sheet of white paper and mark a point O . on this paper. With O as centre draw a circle of any radius.
Step 2: Draw a diameter AB of this circle. Draw any chord AP. Join PB. We thus get ΔAPB such that ∠APB is the angle in a semicircle [see Figure 20.1(a)].

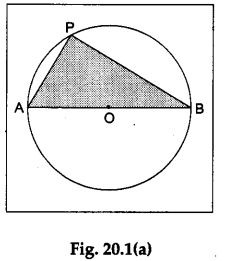
Step 3: Make two exact replicas of A APB using a tracing paper. Make cut-outs of these two replicas of ΔAPB and label them as ΔA₁P₁B₁ and ΔA₂P₂B₂.
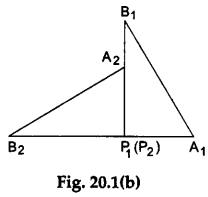
Step 4: Place the two cut-outs adjacent to each other as shown in Figure 20.1(b). What do you observe?

Observations
We observe that the two line segments A₁P₁ and P₂B₂ lie on a straight line.
Therefore, ∠A₁P₁B₁ and ∠A₂P₂B₂ are supplementary angles, i.e., ∠A₁P₁B₁ + ∠A₂P₂B₂ =180°.
Since each of the angles ∠A₁P₁B₁ and ∠A₂P₂B₂ is equal to ∠APB, therefore 2∠APB=180°, i.e., ∠APB = 90°.

Procedure
To verfiy that the angle in a minor segment is an obtuse angle.
Step 1: Take a white sheet of paper and mark a point O on it. With O as centre draw a circle of any radius.
Step 2: Draw a chord MN (such that MN is not a diameter) in this circle.
Step 3: Draw a ΔMQN so that point Q lies on the minor arc of the circle. Thus, ∠MQN is the angle in a minor segment [see Figure 20.2(a)].

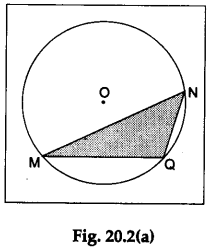
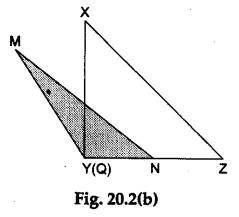
Step 4: Make an exact replica of ΔMQN. Place it over a right-angled ΔXYZ (right angled at point Y) in such a way that side QN of ΔMQN falls over the side YZ of ΔXYZ as shown in Figure 20.2(b). What do you observe?

Observations
∠MQN is greater than ∠XYZ, i.e., ∠MQN > 90°, i.e., ∠MQN is an obtuse angle.
Procedure To verify that the angle in a major segment is an acute angle.
Step 1: Take a white sheet of paper and mark a point O on it. With O as centre draw a circle of any radius.
Step 2: Draw a chord GH (such that GH is not a diameter) in this circle.
Step 3: Draw a ΔGSH so that point S lies on the major arc of the circle. Thus, ∠GSH is the angle in a major segment [see Figure 20.3(a)].

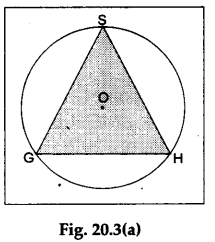
Step 4: Make an exact replica of ΔGSH. Place it over the right-angled ΔXYZ in such a way that side SG of ΔGSH falls over the side YZ of ∠XYZ as shown in Figure 20.3(b). What do you observe?

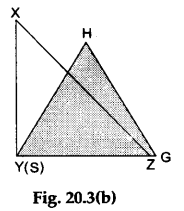
Observations
∠GSH is less than ∠XYZ, i.e., ∠GSH <90°, i.e., ∠GSH is an acute angle.

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs