Math Labs with Activity – The Lengths of the Tangents Drawn from an External Point to a Circle
OBJECTIVE
To verify that the lengths of the tangents drawn from an external point to a circle are equal
Materials Required
- A sheet of transparent paper
- A geometry box
Theory
The theorem can be proved as follows.
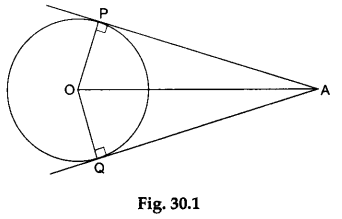
Let two tangents AP and AQ be drawn from a point A (external point) to a circle with its centre at O and having a radius r.
Join OP, OQ and OA.
In AOPA and OQA, we have
- OP=OQ (each is equal to r)
- OA =OA (common)
- ∠OPA = ∠OQA (each is equal to 90° since AP and AQ are tangents).
∴ ΔOPA is congruent to ΔOQA (by RHS-criterion).
Hence, AP = AQ, i.e., the two tangents are equal.
Procedure
Step 1: Mark a point O on the sheet of transparent paper. With O as the centre, draw a circle of any radius.
Step 2: Mark a point A outside the circle.
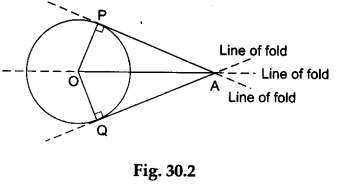
Step 3: Fold the paper along the line that passes through the point A and just touches the circle. Make a crease and unfold the paper. Mark the point P where the line of fold touches the circle. Join AP. Then, AP is one of the tangents to the circle from the point A.
Step 4: Fold the paper along the line that passes through the point A and just touches the circle at a point other than P. Make a crease and unfold the paper. Mark the point Q where the line of fold touches the circle. Join AQ. Then, AQ is another tangent to the circle through the point A.
Step 5: Join OP, OQ and OA, as shown in Figure 30.2.
Step 6: Fold the paper along the line OA.
Observations
We observe that when the paper is folded along the line OA, the point P falls exactly on the point Q. Therefore, AP = AQ.
Result
It is verified that the lengths of the tangents drawn from an external point to a circle are equal.
Math Labs with ActivityMath LabsScience Practical SkillsScience Labs
