Math Labs with Activity - Curved Surface Area of a Right-Circular Cone Formula

Math Labs with Activity – Curved Surface Area of a Right-Circular Cone Formula

OBJECTIVE

To demonstrate a method to derive a formula for finding the curved surface area of a right-circular cone (Method 2)

Materials Required

1. A model of a right-circular cone made of chart paper
2. A pair of scissors
3. A sheet of white paper

Theory
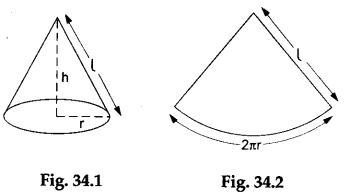
When a cone of slant height l and base radius r made of chart paper (as shown in Figure 34.1) is unfolded, we get a sector of a circular sheet of radius l formed by an arc of length 2πr (as shown in Figure 34.2).

Procedure
Step 1: Take a right-circular cone having slant height l and base radius r as shown in Figure 34.3.

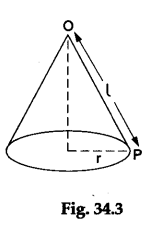
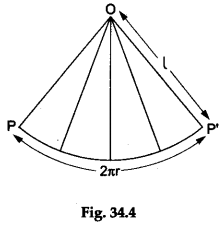
Step 2: Mark a point P on the circular edge of the cone. Mark the vertex of the cone as O. Join OP. Cut the cone along the line OP to get a sector of a circle of radius l formed by an arc of length 2πr.
Step 3: Draw three lines in this sector dividing it into four equal sectors as shown in Figure 34.4.

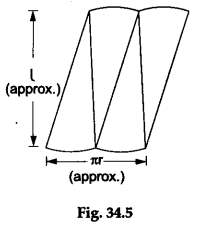
Cut these four sectors and place them adjacent to each other to form a geometrical shape closely resembling a parallelogram as shown in Figure 34.5.

Observations and Calculations
The curved surface area of the cone must be equal to the area of the parallelogram formed.
The approximate area of the parallelogram = base x height = πrl.

Result
The curved surface area of a right-circular cone having slant height l and base radius r is given by πrl.

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs