Math Labs with Activity - Angle Subtended by an Arc at the Centre of a Circle is Double

Math Labs with Activity – Angle Subtended by an Arc at the Centre of a Circle is Double

OBJECTIVE

To verify that the angle subtended by an arc at the centre of a circle is double the angle subtended by it at any point on the remaining part of the circle

Materials Required

1. A sheet of white paper
2. A piece of cardboard
3. A sheet of tracing paper
4. A sheet of colored paper
5. A geometry box
6. A tube of glue

Theory
The theorem may be proved as follows.
Consider a circle with centre O and radius r. Let AB be any arc of this circle. Join AB. Join CO and produce it to a point D outside the circle (see Figure 27.1).

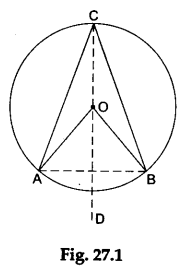
Then, ∠AOD = ∠OAC + ∠ACO and ∠BOD = ∠OBC + ∠BCO.
[When a side of a triangle is produced, the exterior angle is equal to the sum of the opposite interior angles.]
But ∠OAC = ∠ACO      [OC=OA=r]
and ∠OBC = ∠BCO.     [OC=OB=r]
∴ ∠AOD=2 ∠ACO and ∠BOD = 2∠BCO.
∴ ∠AOB = ∠AOD + ∠BOD = 2 ∠ACO + 2 ∠BCO.
= 2 (∠ACO + ∠BCO) = 2 ∠ACB.

Procedure
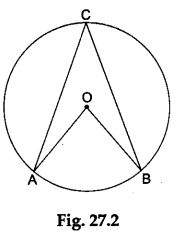
Step 1: Paste the sheet of white paper on the cardboard. Mark a point O on this paper. With O as the centre, draw a circle of any radius.
Step 2: Mark two points A and B on this circle. Then, AB is an arc of the circle. Mark any point C on the remaining part of the circle. Join OA, OB, AC and BC. Then, ∠AOB is the angle subtended by AB at the centre of the circle and ∠ACB is the angle subtended by AB at any point on the remaining part of the circle (see Figure 27.2).

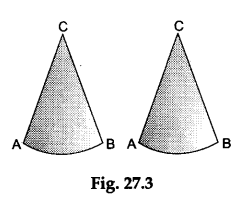
Step 3: Trace ∠ACB on the tracing paper and use it to make two exact copies of ∠ACB on the coloured paper as shown in Figure 27.3.

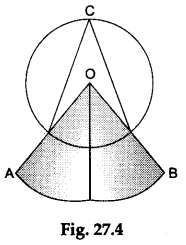
Cut these two copies of ∠ACB. Place them adjacent to each other over ∠AOB as shown in Figure 27.4.

Observations
We observe that the two copies of ∠ACB when placed adjacent to each other exactly cover ∠AOB.
Therefore, ∠AOB = 2 ∠ACB.

Result
It is verified that the angle subtended by an arc at the centre of a circle is double the angle subtended by it at any point on the remaining part of the circle.

Remarks:
If AB is a semicircle then ∠AOB = 180° and so, by the above theorem, ∠ACB = 90°, as shown in Figure 27.5.

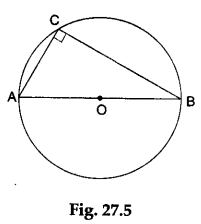
Clearly, ∠ACB is an angle in a semicircle.
We, therefore, conclude that the angle in a semicircle is a right angle.

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs