Math Labs with Activity - Alternate-Segment Theorem

Math Labs with Activity – Alternate-Segment Theorem

OBJECTIVE

To verify the alternate-segment theorem, which states if a chord is drawn through die point of contact of a tangent to a circle then the angles made by this chord with the given tangent are equal respectively to the angles formed in the corresponding alternate segments

Materials Required

1. A sheet of white paper
2. A sheet of tracing paper
3. A geometry box

Theorem
A segment opposite the angle formed by a chord of a circle with the tangent at one of its end points is called the alternate segment for that angle.
In Figure 31.1, AB is a chord and PAT is the tangent to a circle with centre O. The chord AB divides the circle into two segments—ADB and ACB.

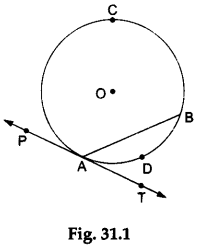
For ∠BAT, the alternate segment is ACB.
For ∠BAP, the alternate segment is ADB. By the alternate-segment theorem,
∠BAT = ∠BCA and ∠BAP = ∠BDA.

Procedure
Step 1: Mark a point O on the sheet of white paper. With O as the centre, draw a circle of any radius.
Step 2: Fold the paper along the line that just touches the circle. Make a crease and unfold the paper. Draw a line PT along the crease. Mark the point A where the line PT touches the circle. Then, PAT is the tangent to the circle at the point A.
Step 3: From A draw a chord AB dividing the circle into a major segment and a minor segment.
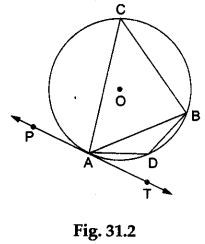
Step 4: Take a point C on the major arc and a point D on the minor arc. Join AC, BC, AD and BD as shown in Figure 31.2.

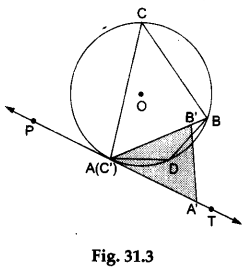
Step 5: Trace ∠BCA on the tracing paper, mark it ∠B’C’A’ and place it over ∠BAT, as shown in Figure 31.3. What do you observe?

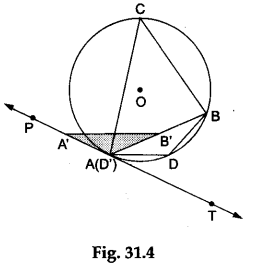
Step 6: Trace ∠BDA on the tracing paper, mark it ∠B’D’A’ and place it over ∠BAP, as shown in Figure 31.4.

Observations
We observe that

1. ∠B’C’A’ exactly covers ∠BAT, i.e., ∠BCA = ∠BAT, and
2. ∠B’D’A’ exactly covers ∠BAP, i.e., ∠BDA = ∠BAP.

Result
The alternate-segment theorem is verified.

Math Labs with ActivityMath LabsScience Practical SkillsScience Labs