What is Logarithmic Series Expansion ?
https://www.youtube.com/watch?v=sC8-Kt_NkEY&t=15s
Logarithmic Series
Definition
An expansion for loge (1 + x) as a series of powers of x which is valid only, when |x|<1.
Expansion of logarithmic series
Expansion of loge (1 + x) if |x|<1 then
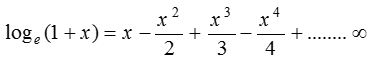
Replacing x by −x in the logarithmic series, we get
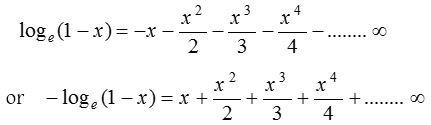
Some Important results from logarithmic series
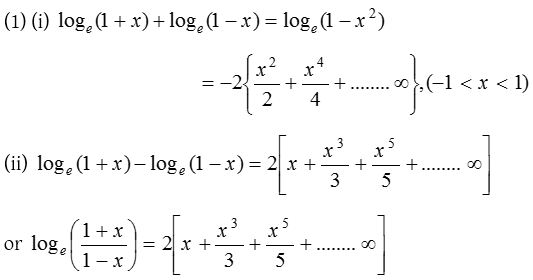
(2) The series expansion of loge (1 + x) may fail to be valid, if |x| is not less than 1. It can be proved that the logarithmic series is valid for x = 1. Putting x = 1 in the logarithmic series.
We get,
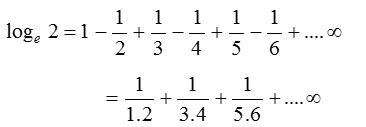
(3) When x = −1, the logarithmic series does not have a sum. This is in conformity with the fact that log(1 – 1) is not a finite quantity.
Difference between the exponential and logarithmic series
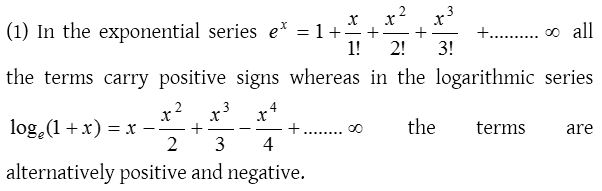
(2) In the exponential series the denominator of the terms involve factorial of natural numbers. But in the logarithmic series the terms do not contain factorials.
(3) The exponential series is valid for all the values of x. The logarithmic series is valid, when |x|< 1.
