Logarithmic Expressions

A logarithm is an exponent.
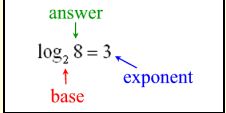
In the example shown above, 3 is the exponent to which the base 2 must be raised to create the answer of 8, or 23 = = 8. In this example, 8 is called the anitlogarithm base 2 of 3.
Read also:
- How do Logarithms Work?
- Logarithmic Equations
- Logarithmic Functions
- What is Logarithmic Series Expansion?

Try to remember the “spiral” relationship between the values as shown at the right. Follow the arrows starting with base 2 to get the equivalent exponential form.

Logarithms with base 10 are called common logarithms.
When the base is not indicated, base 10 is implied.
Logarithms with base e are called natural logarithms.
Natural logarithms are denoted by ln.

On the graphing calculator:
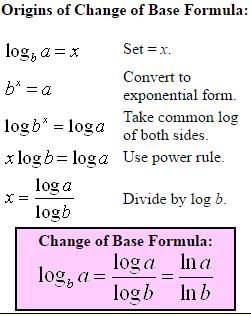
The base 10 logarithm is the log key.
The base e logarithm is the ln key.
To enter a logarithm with a different base,
use the Change of Base Formula:
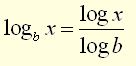
Properties of Logs:
Using the properties of exponents, we can arrive at the properties of logarithms.

Examples:

