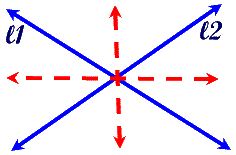
Locus: Equidistant from Two Intersecting Lines
Consider: Indiana Jones (Indy) is searching for a treasure. His treasure map shows a V-shaped canyon formed by two vertical cliffs. The directions state:
“Start at the point where the cliffs converge. Walk through the canyon staying an equal distance from each cliff……”
Can you picture the path Indy needs to take to satisfy these directions?
Description:
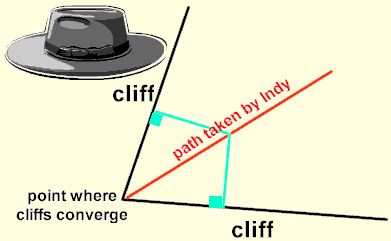 The red line represents the locus which is equidistant from the two cliffs. This line is the bisector of the angle formed by the two cliffs. Any point on this line, when measured as shown by the green lines, is the same distance from each cliff.
The red line represents the locus which is equidistant from the two cliffs. This line is the bisector of the angle formed by the two cliffs. Any point on this line, when measured as shown by the green lines, is the same distance from each cliff.
Formally stated, we have another locus theorem.
Locus Theorem 5: (Intersecting lines)
The locus of points equidistant from two intersecting lines, ?1 and ?2, is a pair of bisectors that bisect the angles formed by ?1 and ?2.