What is a Locus
Locus
A locus is a set of points which satisfies a certain condition.
As seen by the headlights (and taillights) in the picture below, a locus of points (the headlights or taillights) is the path traced out by the moving points under given conditions (following the road).
 Think of a locus as a “bunch” of points that all do the same thing.
Think of a locus as a “bunch” of points that all do the same thing.
In Latin, the word locus means place.
The plural of locus is loci.
There are five basic locus theorems (rules).
Each theorem will be explained in detail in the following sections under this topic. Even though the theorems sound confusing, the concepts are easy to understand.
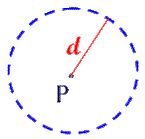
Locus Theorem 1:
The locus of points at a fixed distance, d, from point P is a circle with the given point P as its center and d as its radius.
 Locus Theorem 2:
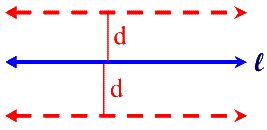
Locus Theorem 2:
The locus of points at a fixed distance, d, from a line ?, is a pair of parallel lines d distance from ? and on either side of ?.
 Locus Theorem 3:
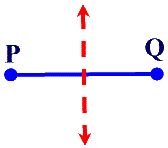
Locus Theorem 3:
The locus of points equidistant from two points, P and Q, is the perpendicular bisector of the line segment determined by the two points.
 Locus Theorem 4:
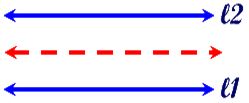
Locus Theorem 4:
The locus of points equidistant from two parallel lines, ?1 and ?2 , is a line parallel to both ?1 and ?2 and midway between them.
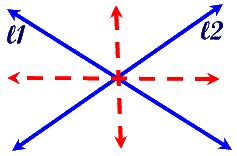
 Locus Theorem 5:
Locus Theorem 5:
The locus of points equidistant from two intersecting lines, ?1 and ?2, is a pair of bisectors that bisect the angles formed by ?1 and ?2 .
When attempting to solve a locus problem, there are certain steps that should be followed:
Steps to solving a locus problem:
- Draw a diagram showing the given lines and points.
- Read carefully to determine the needed condition(s).
- Locate one point that satisfies the needed condition and plot it on your diagram. Locate several additional points that satisfy the condition and plot them as well. Plot enough points so that a pattern (a shape, a path) is starting to appear.
- Through these plotted points draw a dotted line to indicate the locus (or path) of the points.
- Describe in words the geometric path that appears to be the locus.
- If TWO conditions exist in your problem (a compound locus), repeat steps 2-4 above for the second condition ON THE SAME DIAGRAM. Count the number of points where the two loci intersect. (Where do the dotted lines cross?)
