What is a Linear Regression Model?
Linear regression
If a relation between two variates x and y exists, then the dots of the scatter diagram will more or less be concentrated around a curve which is called the curve of regression. If this curve be a straight line, then it is known as line of regression and the regression is called linear regression.
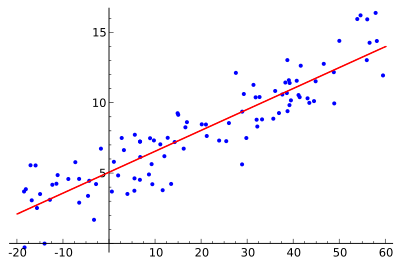
Line of regression: The line of regression is the straight line which in the least square sense gives the best fit to the given frequency.
Equations of lines of regression
(1) Regression line of y on x : If value of x is known, then value of y can be found as
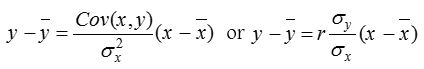
(2) Regression line of x on y : It estimates x for the given value of y as
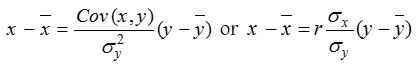
(3) Regression coefficient :
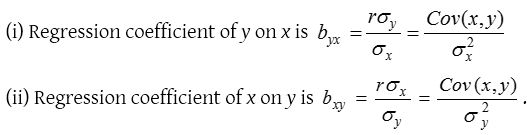
Angle between two lines of regression
Equation of the two lines of regression are
![]()
We have,
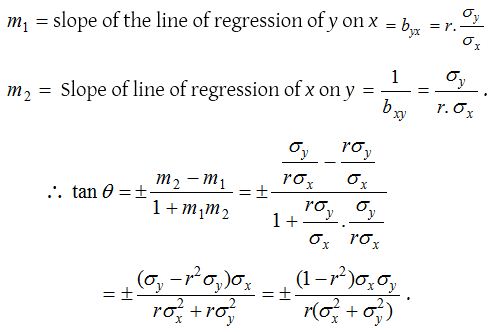
Here the positive sign gives the acute angle θ, because r2 ≤ 1 and σx, σy are positive.
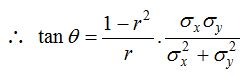
If r = 0, from (i) we conclude tan θ = ∞ or θ = π/2 i.e., two regression lines are at right angles.
If r = ±1, tan θ = 0 i.e., θ = 0, since θ is acute i.e., two regression lines coincide.
Important points about regression coefficients bxy and byx
(1) \(r=\sqrt { { b }_{ xy }.{ b }_{ yx } }\) i.e., the coefficient of correlation is the geometric mean of the coefficient of regression.
(2) If byx > 1, then bxy < 1 i.e., if one of the regression coefficient is greater than unity, the other will be less than unity.
(3) If the correlation between the variable is not perfect, then the regression lines intersect at \((\bar { x } ,\bar { y } )\).
(4) byx is called the slope of regression line y on x and \(\frac { 1 }{ { b }_{ xy } }\) is called the slope of regression line x on y.
(5) \({ b }_{ yx }+{ b }_{ xy }>2\sqrt { { b }_{ yx }{ b }_{ xy } }\) or \({ b }_{ yx }+{ b }_{ xy }>2r\) i.e., the arithmetic mean of the regression coefficients is greater than the correlation coefficient.
(6) Regression coefficients are independent of change of origin but not of scale.
(7) The product of lines of regression’s gradients is given by \(\frac { { \sigma }_{ y }^{ 2 } }{ { \sigma }_{ x }^{ 2 } }\).
(8) If both the lines of regression coincide, then correlation will be perfect linear.
(9) If both byx and bxy are positive, the will be positive and if both byx and bxy are negative, the r will be negative.
