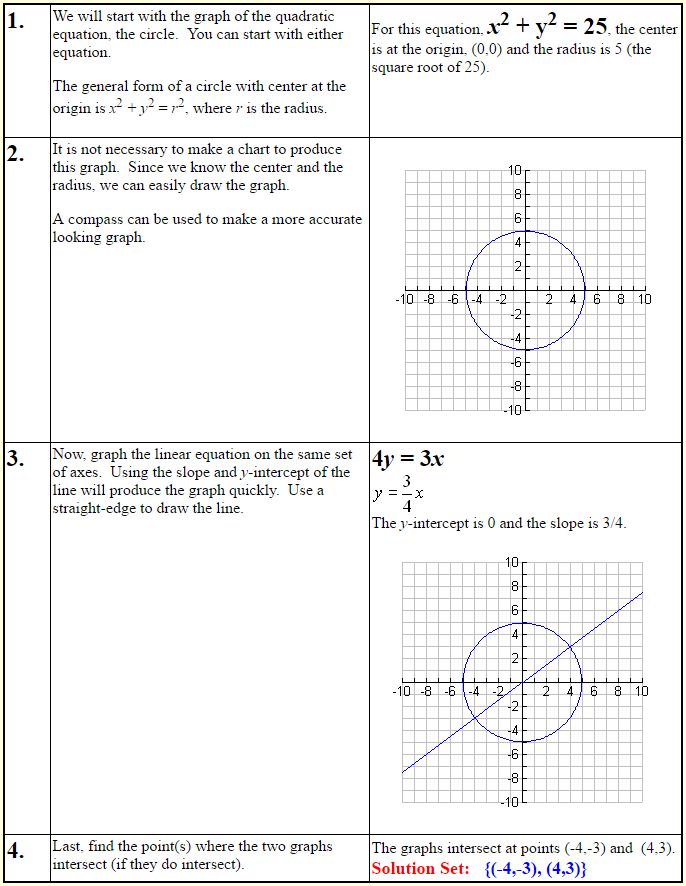
Linear – Quadratic Systems
A quadratic equation is defined as an equation in which one or more of the terms is squared but raised to no higher power. The general form is ax2 + bx + c = 0, where a, b and c are constants.
In Algebra and Geometry, we learned how to solve linear – quadratic systems algebraically and graphically. With our new found knowledge of quadratics, we are now ready to attack problems that cannot be solved by factoring, and problems with no real solutions.
Linear – quadratic system: (where the quadratic is in one variable – only one variable is squared)
y = x – 2 (linear)
y = x2 – 4x – 2 (quadratic – a parabola)
This familiar linear- quadratic system, where only one variable is squared in the quadratic, will be the graph of a parabola and a straight line. When a parabola and a straight line are graphed on the same set of axes, three situations are possible.
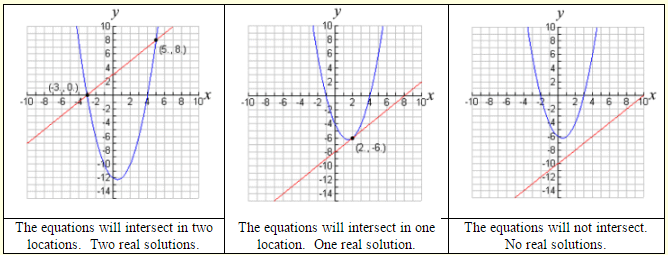
Keep these images in mind as we proceed to solve these linear-quadratic systems algebraically.
Example 1:
When we studied these systems in Algebra, we encountered situations that could be solved by factoring, such as this first example.
Solve this system of equations algebraically:

Example 2:
Solve this problem manually (without graphing calculator):
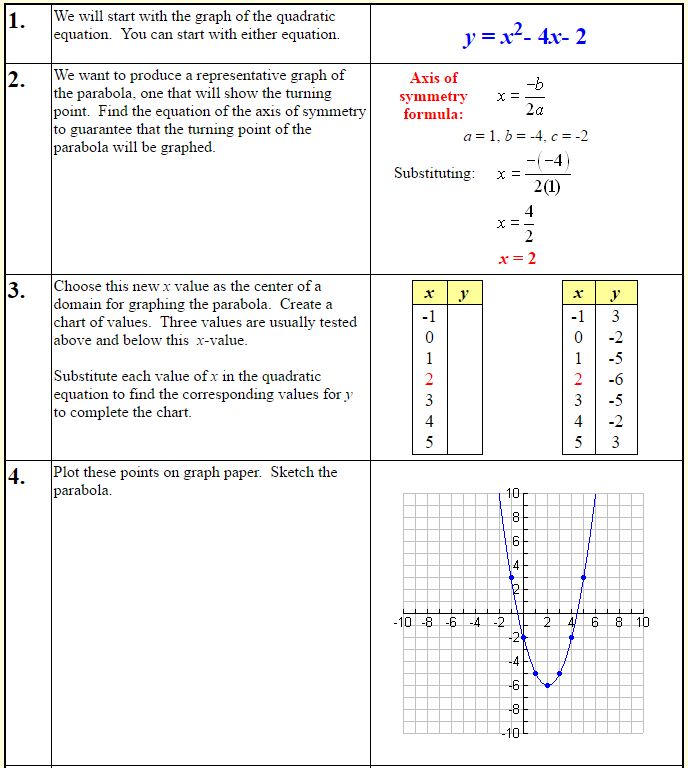
y = x2 – 4x – 2
y = x – 2
Solution:
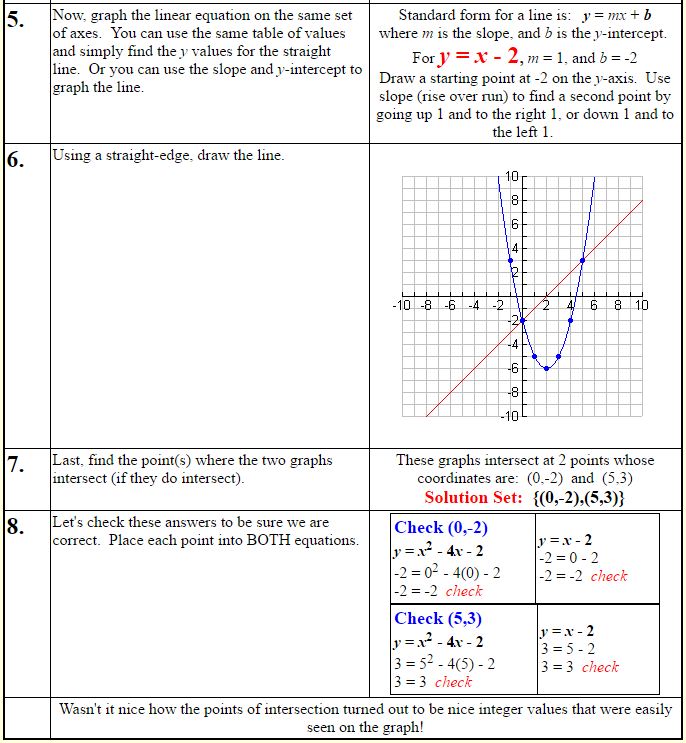
The problem we just solved worked out “nicely” since the intersection points were easily seen as integer values on the graph paper. Of course, this does not happen with all graphs. How could we tell, by looking at the graph, if a point of intersection was (2.3, 1.5), for example?
Answer: We could not tell “by looking”. We would have to solve the system algebraically to find such an intersection point, or we would have to use our graphing calculator with the intersect option.
Example 3:
Solve this problem using a graphing calculator:
y = x2 + x – 1
y = -2x + 1
Solution:

Example 4:
Linear – quadratic system: (where the quadratic is in two variables – both variables are squared)
4y = 3x (linear)
x2 + y2 = 25 (quadratic – a circle)
Solution:
Solve this problem manually (without graphing calculator):