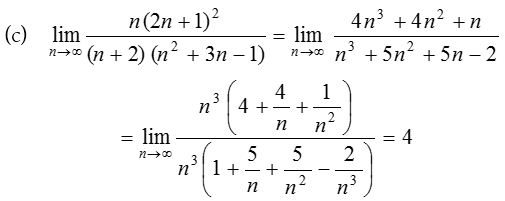Limits (An Introduction)
Limit of a function
Let y = f(x) be a function of x. If at x = a, f(x) takes indeterminate form, then we consider the values of the function which are very near to ‘a’. If these values tend to a definite unique number as x tends to ‘a’, then the unique number so obtained is called the limit of f(x) at x = a and we write it as
![]()
Left hand and right hand limit
Consider the values of the functions at the points which are very near to a on the left of a. If these values tend to a definite unique number as x tends to a, then the unique number so obtained is called left-hand limit of f(x) at x = a and symbolically we write it as
![]()
Similarly we can define right-hand limit of f(x) at x = a which is expressed as
![]()
Method for finding L.H.L. and R.H.L.
(i) For finding right hand limit (R.H.L.) of the function, we write x + h in place of x, while for left hand limit (L.H.L.) we write x – h in place of x.
(ii) Then we replace x by ‘a’ in the function so obtained.
(iii) Lastly we find limit h → 0.
Existence of limit
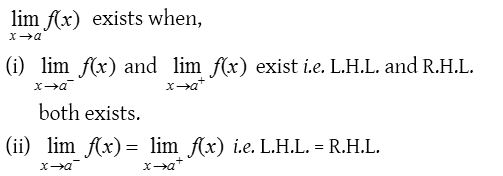
Fundamental theorems on limits

Limits Problems with Solutions
1.
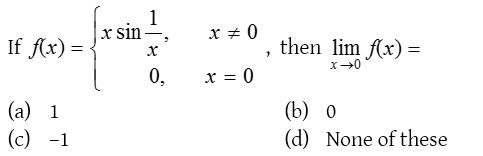
Solution:
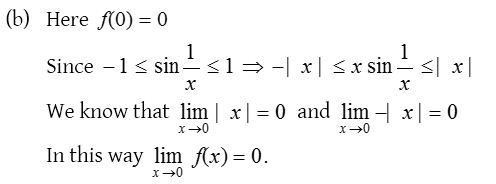
2.
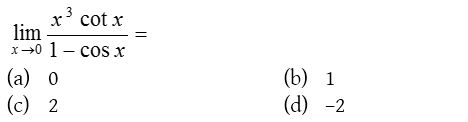
Solution:
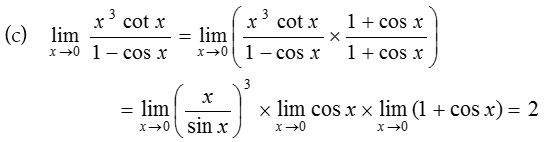
3.
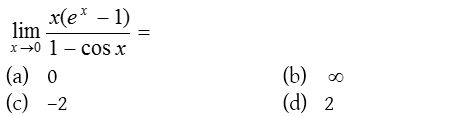
Solution:
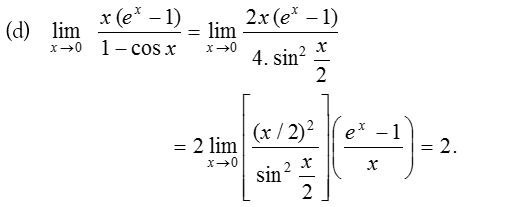
4.
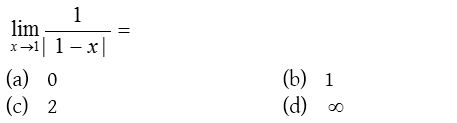
Solution:
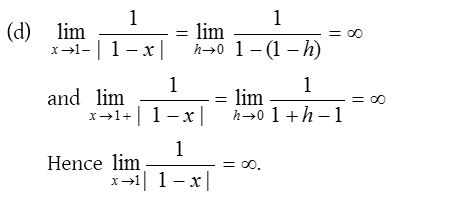
5.
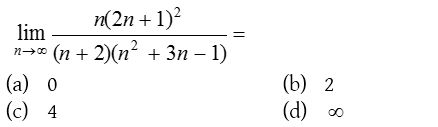
Solution: