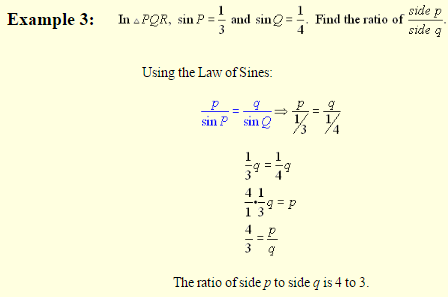Law of Sines
When you see the triangle below on the left and someone asks you to find the value of x, you immediately know how to proceed. You call upon your friend the Pythagorean Theorem because you see the right angle.
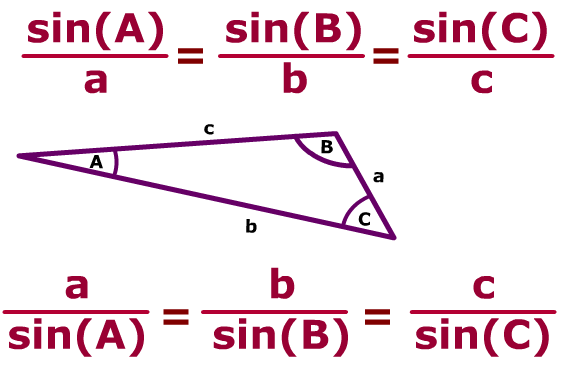But what do you do when you see the triangle on the right? There is no indication of a right angle.
Now, with our knowledge of trigonometry, we are armed to attack any of these perplexing problems!
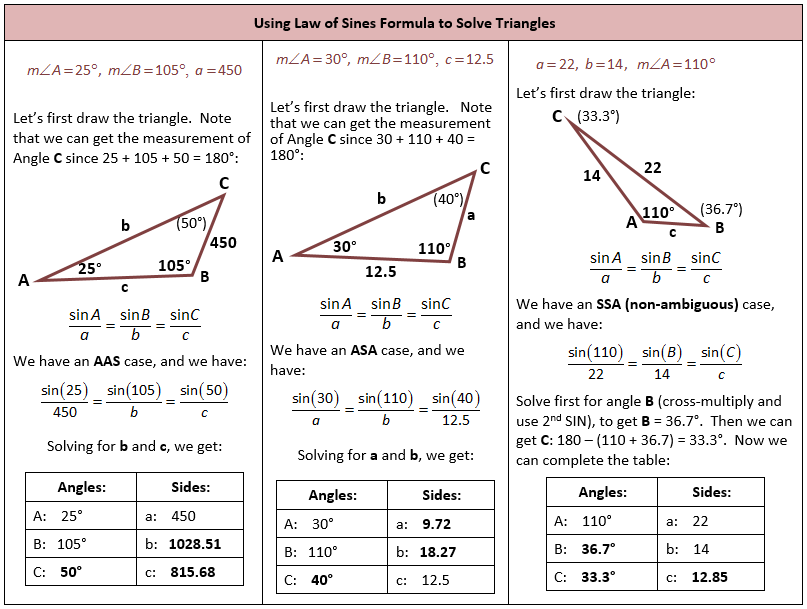
Let’s see how to apply trigonometry to working in triangles which do not contain a right angle.
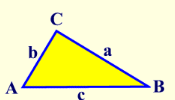
In this diagram, notice how the triangle is labeled. The capital letters for the vertices are repeated in small case on the side opposite the corresponding vertex.
side a is opposite <A
side b is opposite <B
side c is opposite <C
The ratios of each side to the sine of its “partner” are equal to each other.
These ratios, in pairs, are applied to solving problems. You never need to use all three ratios at the same time. Mix and match the ratios to correspond with the letters you need. Remember when working with proportions, the product of the means equals the product of the extremes (cross multiply).
