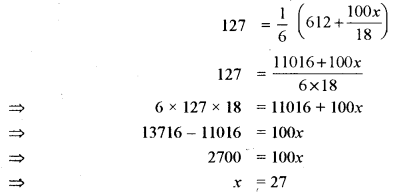ISC Maths Question Paper 2013 Solved for Class 12

ISC Maths Previous Year Question Paper 2013 Solved for Class 12

Time Allowed: 3 Hours
Maximum Marks: 100

(Candidates are allowed additional 15 minutes for only reading the paper. They must NOT start writing during this time.)

• The Question Paper consists of three sections A, B and C.
• Candidates are required to attempt all questions from Section A and all questions either from Section B or Section C.
• Section A: Internal choice has been provided in three questions of four marks each and two questions of six marks each.
• Section B: Internal choice has been provided in two questions of four marks each.
• Section C: Internal choice has been provided in two questions of four marks each.
• All working, including rough work, should be done on the same sheet as, and adjacent to the rest of the answer.
• The intended marks for questions or parts of questions are given in brackets [ ].
• Mathematical tables and graph papers are provided.

Section – A
(All questions are compulsory in this part)

Question 1.
(i) If (A – 2I) (A – 3I) = 0, where \(A=\left(\begin{array}{cc}{4} & {2} \\ {-1} & {x}\end{array}\right) \text { and } I=\left(\begin{array}{ll}{1} & {0} \\ {0} & {1}\end{array}\right)\), find the value of x. [3]
(ii) Find the value (s) of k so that the line 2x + y + k = 0 may touch the hyperbola 3x² – y² = 3. [3]
(iii) Prove that: \(\tan ^{-1} \frac{1}{4}+\tan ^{-1} \frac{2}{9}=\frac{1}{2} \sin ^{-1} \frac{4}{5}\) [3]
(iv) Using L’Hospital’s Rule, evaluate: [3]
\(\lim _{x \rightarrow 0}\left(\frac{e^{x}-e^{-x}-2 x}{x-\sin x}\right)\)
(v) Evaluate: \(\int \frac{1}{x+\sqrt{x}} d x\) [3]
(vi) Evaluate: \(\int_{0}^{1} \log \left(\frac{1}{x}-1\right) d x\) [3]
(vii) Two regression lines are represented by 4x + 10y = 9 and 6x + 3y = 4. Find the line of regression of y on x. [3]
(viii) If 1, w and w² are the cube roots of unity, evaluate: (1 – w⁴ + w⁸) (1 – w⁸ + w¹⁶) [3]
(ix) Solve the differential equation: [3]
\(\log \left(\frac{d y}{d x}\right)=2 x-3 y\)
(x) If two balls are drawn from a bag containing three red balls and four blue balls, find the probability that: [3]
(a) They are of the same colour
(b) They are of different colours
Solution:

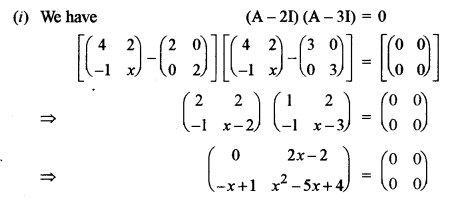
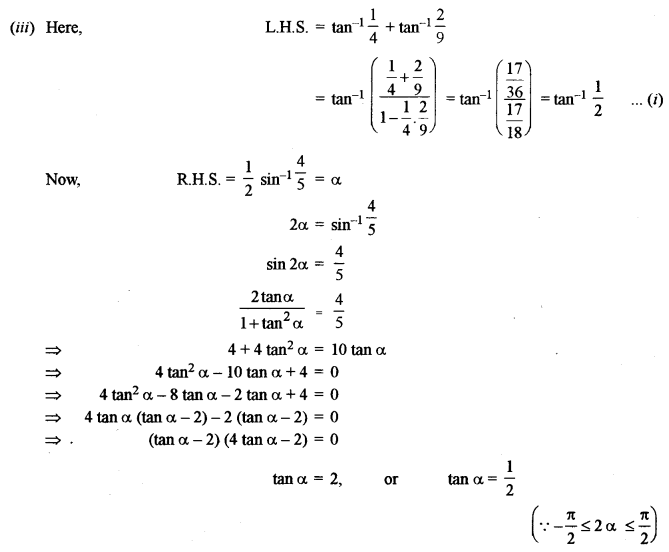
Question 2.
(a) Using properties of determinants, prove that: [5]
\(\left|\begin{array}{ccc}{x} & {y} & {z} \\ {x^{2}} & {y^{2}} & {z^{2}} \\ {y+z} & {z+x} & {x+y}\end{array}\right|=(x-y)(y-z)(z-x)(x+y+z)\)
(b) Find A^-1, where \(A=\left[\begin{array}{ccc}{4} & {2} & {3} \\ {1} & {1} & {1} \\ {3} & {1} & {-2}\end{array}\right]\)
Hence, solve the following system of linear equations: [5]
4x + 2y + 3z = 2
x + y + z = 1
3x + y – 2z = 5
Solution:

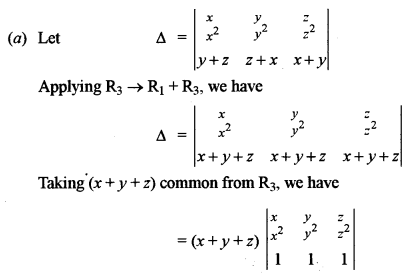
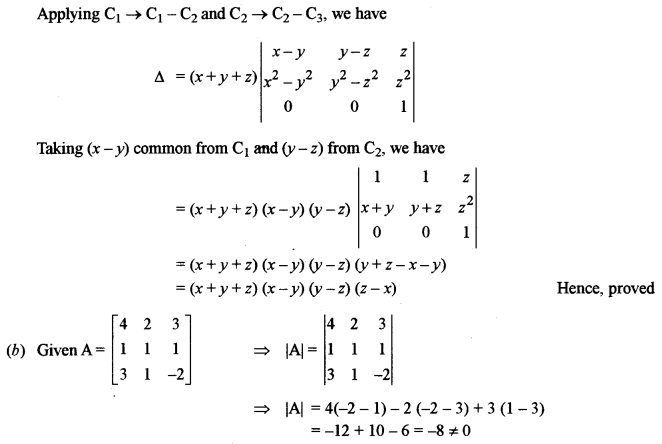
Question 3.
(a) Solve for x: \(\sin ^{-1} x+\sin ^{-1}(1-x)=\cos ^{-1} x\). [5]
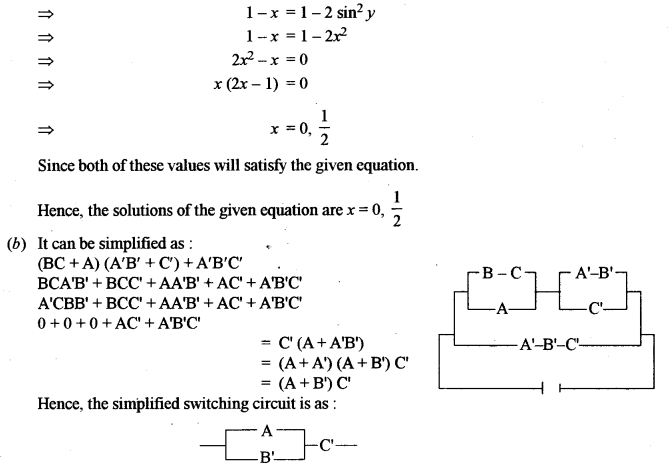
(b) Construct a circuit diagram for the following Boolean Function:
(BC + A) (A’B’ + C) + A’B’C’
Using laws of Boolean Algebra, simplify the function and draw the simplifed circuit. [5]
Solution:

Question 4.
(a) Verify Lagrange’s Mean Value Theorem for the function \(f(x)=\sqrt{x^{2}-x}\) in the interval [1, 4]. [5]
(b) From the following information, find the equation of the Hyperbola and the equation of its Transverse Axis.
Focus: (-2, 1), Directrix: 2x – 3y + 1 = 0, \(e=\frac{2}{\sqrt{3}}\) [5]
Solution:



Which is the required equation of the hyperbola
Transverse axis is ⊥ to directrix
Equation of transverse axis be 3x + 2y + k = 0 ……(ii)
Focus (-2, 1) lies on transverse axis
3 × (-2) + 2 × 1 + k = 0
⇒ -4 + k = 0
⇒ k = 4
Now putting the value of k = 4 in (ii), we have
Equation of transverse axis is 3x + 2y + 4 = 0

Question 5.
(a) If y = (cot^-1x)², show that \(\left(1+x^{2}\right)^{2} \frac{d^{2} y}{d x^{2}}+2 x\left(1+x^{2}\right) \frac{d y}{d x}=2\) [5]
(b) Find the maximum volume of the blinder which can be inscribed in a sphere of radius 3√3 cm. (Leave the answer in terms of π).
Solution:

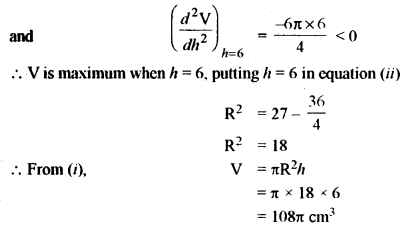
Question 6.
(a) Evaluate: \(\frac{\cos ^{-1} x}{x^{2}} d x\) [5]
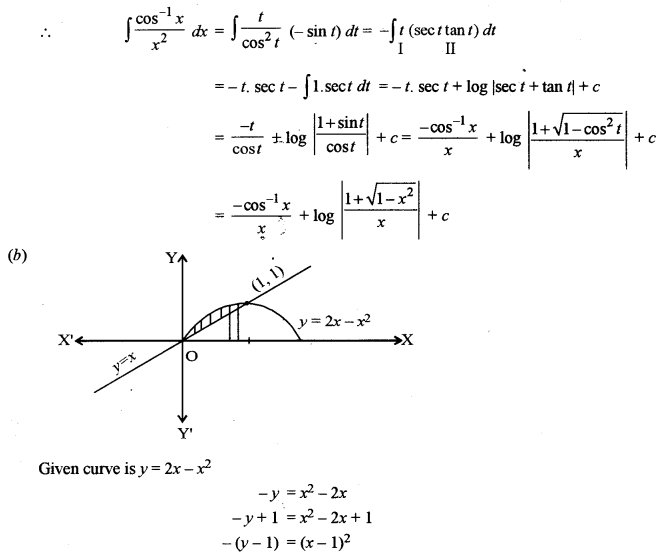
(b) Find the area bounded by the curve y = 2x – x², and the line y = x. [5]
Solution:
(a) Put cos^-1x = t
⇒ x = cos t
⇒ dx = -sin t dt

Question 7.
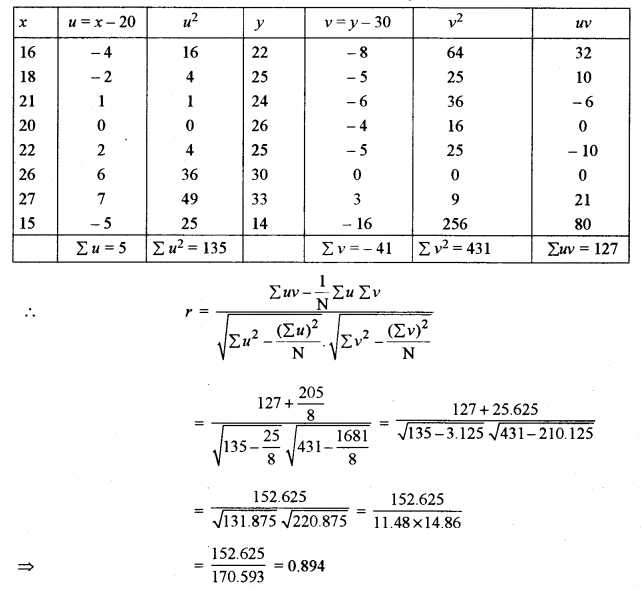
(a) Find Karl Pearson’s coefficient of correlation between x and y for the following data: [5]

(b) The following table shows the mean and standard deviation of the marks of Mathematics and Physics scored by the students in a School: [5]

The correlation coefficient between the given marks is 0.86. Estimate the likely marks in Physics if the marks in Mathematics are 92.
Solution:
(a) Assume mean A = 20 for the x-variate and B = 30 for the y-variate.

Question 8.
(a) Bag A contains three red and four white Balls; bag B contains two red and three white Balls. If one ball is drawn from bag A and two Balls from bag B, find the probability that: [5]
(i) One ball is red and two balls are white
(ii) All the three balls are of the same colour.
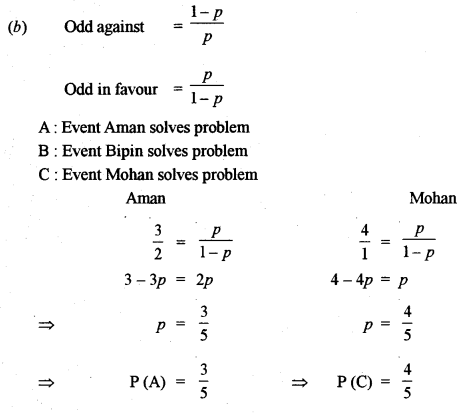
(b) Three persons, Aman, Bipin and Mohan attempt a Mathematics problem independently. The odds in favour of Aman and Mohan solving the problem are 3 : 2 and 4 : 1 respectively and the odds against Bipin solving the problem are 2 : 1. Find: [5]
(i) The probability that all three will solve the problem.
(ii) The probability that the problem will be solved.
Solution:
(a) Here, the possible selection is as follows:
(i) 1 Red from bag A, 2 white from bag B
1 White from bag A, 1 white from bag B 1 Red from B
P (one ball is red and two balls are white)

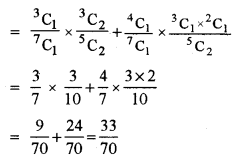
(ii) Possible selection is as follows:
(a) 1 Red from Bag A, 2 Red from Bag B
(b) 1 White from Bag A, 2 white from Bag B
P (All the three balls are of the same colour)

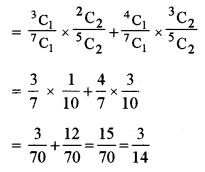
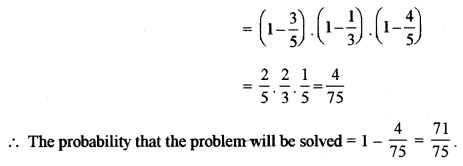
Question 9.
(a) Find the locus of the complex number z = x + iy, satisfying relations arg (z – 1) = \(\frac{\pi}{4}\) and |z – 2 – 3i| = 2. Illustrate the locus oh the Argand plane. [5]
(b) Solve the following differential equation:
\(y e^{y} d x=\left(y^{3}+2 x e^{y}\right) d y\), given that x = 0, y = 1 [5]
Solution:

Section – B

Question 10.
(a) If \(\vec{a} \text { and } \vec{b}\), are unit vectors and 0 is the angle between them, then show that \(|\vec{a}-\vec{b}|=2 \sin \frac{\theta}{2}\). [5]
(b) Find the value of λ for which the four points A, B, C, D with position vectors \(-\hat{j}-\hat{k} : 4 \hat{i}+5 \hat{j}+\lambda \hat{k} : 3 \hat{i}+9 \hat{j}+4 \hat{k} \text { and }-4 \hat{i}+4 \hat{j}+4 \hat{k}\) are coplanar. [5]
Solution:

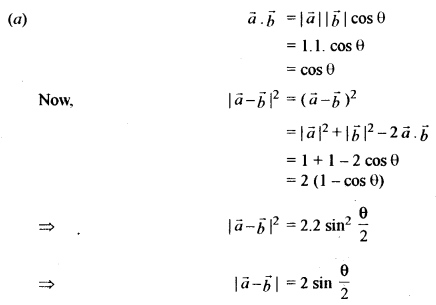
Question 11.
(a) Find the equation of a line passing through the point (-1, 3 -2) and perpendicular to the lines: [5]
\(\frac{x}{1}=\frac{y}{2}=\frac{z}{3} \text { and } \frac{x+2}{-3}=\frac{y-1}{2}=\frac{z+1}{5}\)
(b) Find the equation of planes parallel to the plane 2x – 4y + 4z = 7 and which are at a distance of five units from the point (3, -1, 2). [5]
Solution:
(a) Any line through the point (-1, 3 -2) with direction ratios a, b, c is

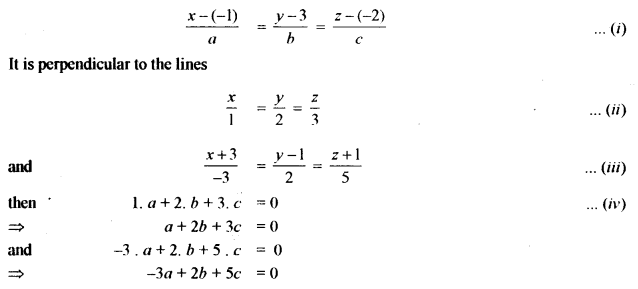
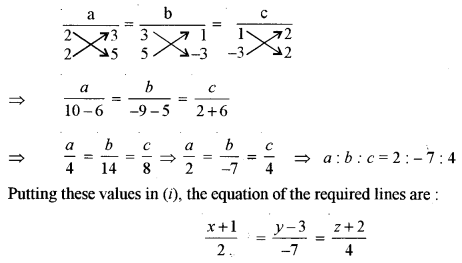
Question 12.
(a) If the sum and the product of the mean and variance of a Binomial Distribution are 1.8 and 0.8 respectively, find the probability distribution and the probability of at least one success. [5]
(b) For A, B and C, the chances of being selected as the manager of a firm are 4 : 1 : 2, respectively. The probabilities for them to introduce a radical change in the marketing strategy are 0.3, 0.8 and 0.5 respectively. If a change takes place; find the probability that it is due to the appointment of B. [5]
Solution:
(a) According to statement of the question, we have
np + npq = 1.8
⇒ np(1 + q) = 1.8 … (i)
and np × npq = 0.8
⇒ n²p²q = 0.8 …..(ii)
Divide the square of (i) by (ii), we obtain

Section – C

Question 13.
(a) If Mr Nirav deposits ₹ 250 at the beginning of each month in an account that pays an interest of 6% per annum compounded monthly, how many months will be required for the deposit to amount to at least ₹ 6390? [5]
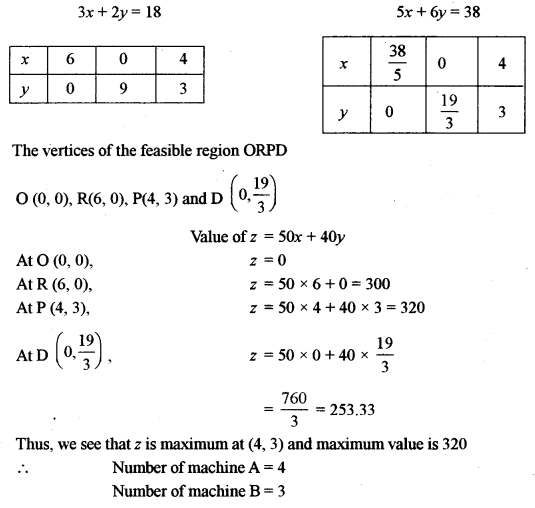
(b) A mill owner buys two types of machines A and B for his mill. Machine A occupies 1000 sq.m of the area and required 12 men to operate it; while machine B occupies 1200 sq.m of the area and requires 8 men to operate it. The owner has 7600 sqm of the area available and 72 men to operate the machines. If machine A produces 50 units and machine B produces 40 units daily, how many machines of each type should he buy to maximise the daily output? Use Linear Programming to find a solution. [5]
Solution:

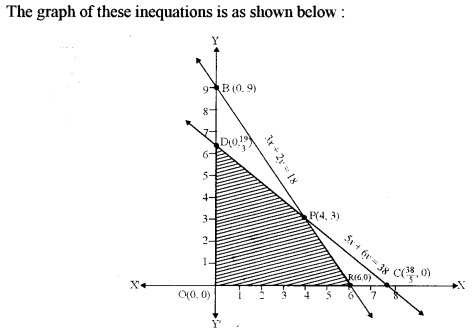
Question 14.
(a) A bill of ₹ 60000 was drawn on 1 st April 2011 at 4 months and discounted for ₹ 58560 at a bank. If the rate of interest was 12% per annum, on what date was the bill discounted? [5]
(b) A company produces a commodity with ₹ 24000 fixed costs. The variable cost is estimated to be 25% of the total revenue recovered on selling the product at a rate of ₹ 8 per unit. Find the following: [5]
(i) Cost function
(ii) Revenue function
(iii) Break-even point.
Solution:
(a) B.D. = Face value – Amount received = ₹ (60000 – 58560) = ₹ 1440
Now, B.D. is interest on face value for remaining periods.
1440 = 60000 × \(\frac { 12 }{ 100 }\) × Remaining period
⇒ Remaining period
\(\begin{array}{l}{=\frac{1440}{12 \times 600} \text { years }=\frac{1}{5} \text { years }} \\ {=\frac{1}{5} \times 365 \text { days }=73 \text { days }}\end{array}\)
Now, bill was drawn on 1st April, 2011 for four months. So legally due date is 4th of August 2011.
The bill was encashed 73 days before this counting days backwards.
August – 4 days
July – 31 days
June – 30 days
May – 8 days
The bill was encashed on (31 – 8) = 23 May, 2011
(b) Suppose that x number of unit are produced and sold.
(i) As each unit’s variable cost is 25% of revenue
The variable cost of x units = 25 % of ₹ 8 x = ₹ 2x
Total cost of producing x units C(x) = TFC + TVC = ₹ (24000 + 2x)
(ii) Price of one unit = ₹ 8
Total revenue on selling x units = R(x) = ₹ 8x
(iii) At break even values
C(x) = R(x)
⇒ 24000 + 2x = 8x
⇒ 24000 = 6x
⇒ x = 4000

Question 15.
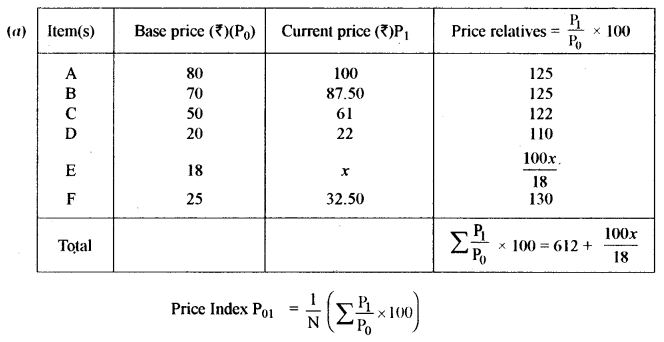
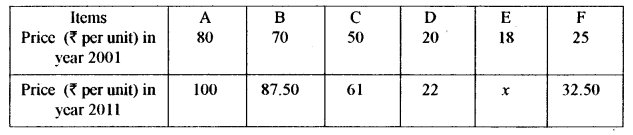
(a) The price index for the following data for the year 2011 taking 2001 as the base year was 127. The simple average of price relatives method was used. Find the value of x. [5]

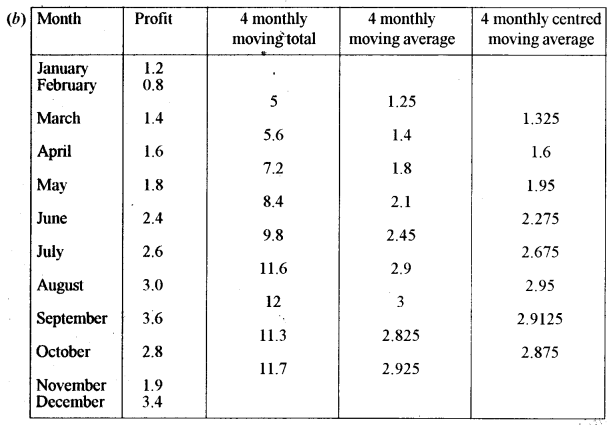
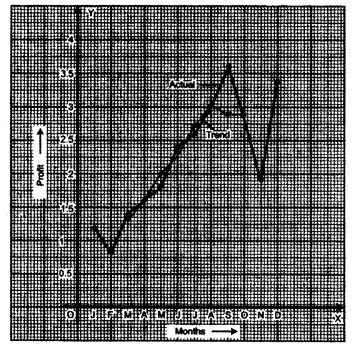
(b) The profits of a paper bag manufacturing company (in lakhs of rupees) during each month of a year are: [5]

Plot the given data on a graph sheet. Calculate the four monthly moving averages and plot these on the same graph sheet.
Solution:

ISC Class 12 Maths Previous Year Question Papers