ISC Computer Science Previous Year Question Paper 2011 Solved for Class 12
Maximum Marks: 70
Time allowed: 3 hours
Part – I
Answer all questions
While answering questions in this Part, indicate briefly your working and reasoning, wherever required.
Question 1.
(a) State the two Absorption laws. Verify any one of them using the truth table. [2]
(b) Reduce the following expression: [2]
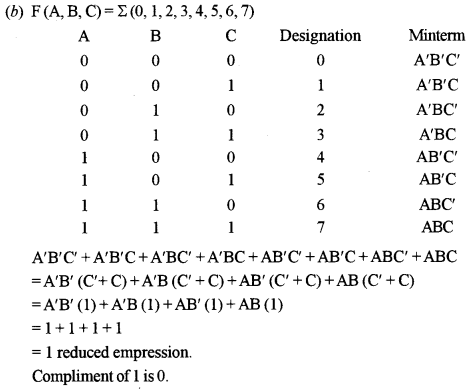
F(A, B, C) = Σ (0, 1, 2, 3, 4, 5, 6, 7)
Also, find the complement of the reduced expression.
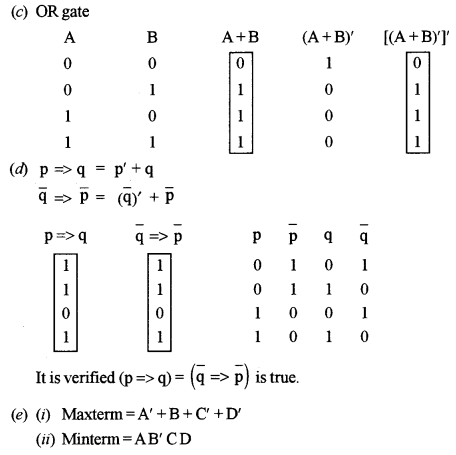
(c) Name the logic gate for the following circuit diagram and write its truth table. [2]
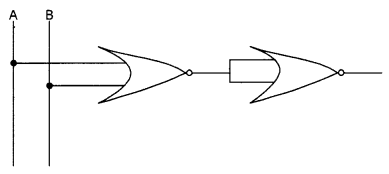
(d) Using truth table, verify whether the following is true or false: [2]
(p⇒q)=(¯q⇒¯p)
(e) If A = 1, B = 0, C= 1 and D = 1 find its: [2]
(i) Maxterm
(ii) Minterm
Answer:

Question 2.
(a) How can we override a method in inheritance? [2]
(b) A square matrix A[m*m] is stored in the memory with each element requiring 2 bytes of storage.
If the base address A[1] [1] is 1098 and the address at A [4] [5] is 1144, determine the order of the matrix A[m × m] when the matrix is stored Column Major wise. [2]
(c) What is Big O notation? [2]
(d) What is an exception? [2]
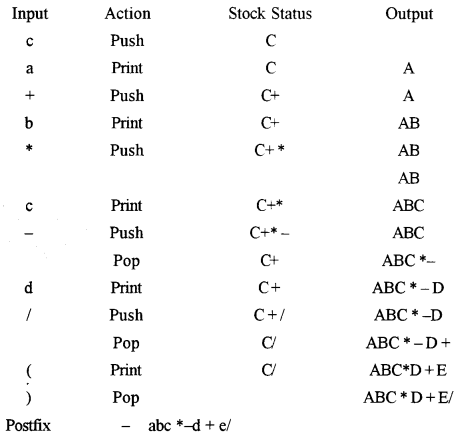
(e) Convert the following infix expression to its postfix form: [2]
a + b * c – d/e
Answer:
(a) When we extend a class, you can change the behaviour of a method in the parent class. This is called method overriding. This happens when we write in a subclass a method that has the same signature as a method in the parent class.
(b) B = 1098, W = 2, n = m
1144 = 1098 + 2 [m(5 – 1) + (4 – 1)]
⇒ 1144 = 1098 + 8m + 6
⇒ 8m = 40
⇒ m = 5
The order of the matrix is [5 × 5]
(c) Big O is the function with parameter N, where N is usually the size of the input to the algorithm. More the input size, more impact it can have on the growth rate of the algorithm.
(d) An unexpected situation or unexpected error, during program execution, is known as an exception.
(e) (a + b * c – d/e)
Question 3.
(a) The following is a part of some class. What will be the output of the function mymethod( ) when the value of the counter is equal to 3? Show the dry run/working. [5]
void mymethod (int counter)
{
if (counter == 0)
System.out. println(” ");
else
{
System.out.println ("Hello" +counter);
mymethod (--counter);
System.out.println (" " +counter);
}
}(b) The following function is a part of some class which computes and returns the greatest common divisor of any two numbers. There are some places in the code marked by ?1?, ?2?, ?3?, ?4? and ?5? which must be replaced by statement/expression so that the function works correctly0
int gcd(int a, int b)
{
int r.
while(?1?)
{
r = ?2?;
b = ?3?;
a = ?4?
}
if (a ==0)
return ?5?;
else
return-1;
}(i) What is the expression or statement at ?1? [1]
(ii) What is the expression or statement at ?2? [1]
(iii) What is the expression or statement at ?3? [1]
(iv) What is the expression or statement at ?4? [1]
(v) What is the expression or statement at ?5? [1]
Answer:

(b) (i) a * b! = 0
(ii) b
(iii) a
(iv) a%b
(v) r
Part – II
Answer seven questions in this part, choosing three questions from Section A, two from Section B and two from Section C.
Section – A
Answer any three questions
Question 4.
(a) State the principle of Duality. Give the dual of the following: [3]
(A’.B) + (C. 1) = (A’ + C).(B + C)
(b) Reduce the Boolean expressions to their simplest forms: [4]
(i) {(C.D)’ +A} + A + C.D + A.B
(ii) A. {B + C(A.B + A. C)’}
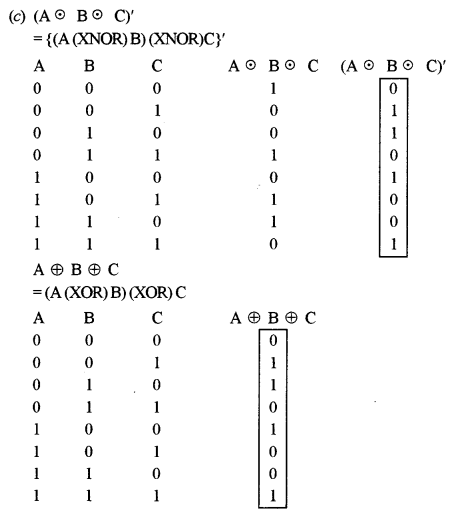
(c) Verily using a truth table if: [3]
(A⊙B⊙C)′=A⊕B⊕C
Answer:
(a) According to the principle of Duality, “Dual of one expression is obtained by replacing AND (.) with OR (+) and OR with AND togather with replacement of 1 with 0 and 0 with 1.”
Dual of (A’ . B) + (C.1) is given by (A’ + B). (C + 0) = (A’ + B). C
Dual of (A’ + C). (B + C) is given by (A’.C) + (B.C)
Then Dual of (A’ . B) + (C . 1) = (A’ + C) . (B + C) is (A’ + B). (C + 0) = (A’.C) + (B.C)
(b) (i) {(C.D)’ + A) + A + C. D + A.B
= {(C.D)’ + A} + A + AB + C.D
= {(C.D)’ + A) + A + C.D [Absorption Law]
= (C’ + D’) + A + A + C.D [De Morgan’s Theorem]
= C’ + D’ + A + C.D
= C’ + C”.D + D’ + A
= C’ + D + D’ + A
= C’ + A
(ii) A. {B + C (A . B + A. C)’}
= A {B + C ((A.B)’ . (A.C)’)} [De Morgan’s theorem]
= A. {B + C ((A’ + B’). (A’ + C’))} [De Morgan’s theorem]
= A. {B + C(A’+B’C’)} [Distributive law]
= A. {B + C.A’ + B’.C’.C.}
= A. (B + C.A’ +0) [Complement property]
= AB + C.A’.A [Complement property]
= AB + 0
= AB
Question 5.
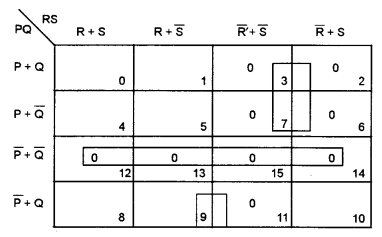
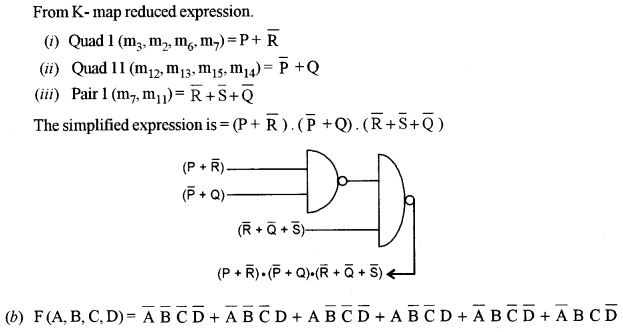
(a) Given F(P, Q, R, S) = Π (2, 3, 6, 7, 9, 11, 12, 13, 14, 15) [5]
Reduce the above expression by using four variable Karnaugh’s Map. Draw the logic gate diagram of the reduced expression using NOR gate only.
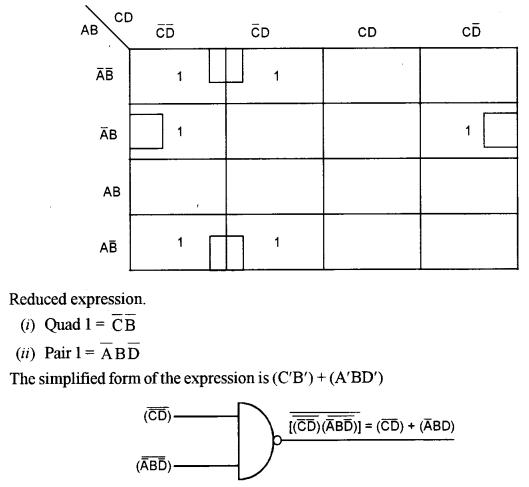
(b) Given F(A,B,C,D)=¯A¯B¯C¯D+¯A¯B¯CD+A¯B¯C¯D+A¯B¯CD+¯AB¯C¯D+¯ABC¯D
Reduce the above expression by using four variable Karnaugh’s Map. Draw the logic gate diagram of the reduced expression using NAND gate only. [5]
Answer:
(a) F (P, Q, R, S) = Π (2, 3, 6, 7, 9, 11, 12, 13, 14, 15)
Question 6.
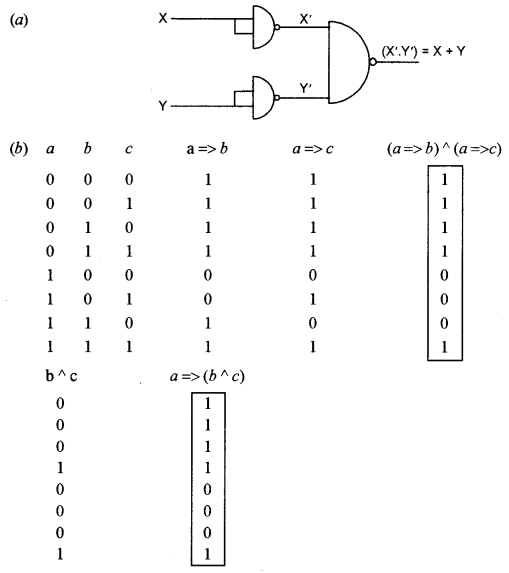
(a) Show with the help of a logic diagram how a NAND gate is equivalent to an OR gate. [3]
(b) Verify if the following is valid: [3]
(a => b)^(a => c) = a => (b ^ c)
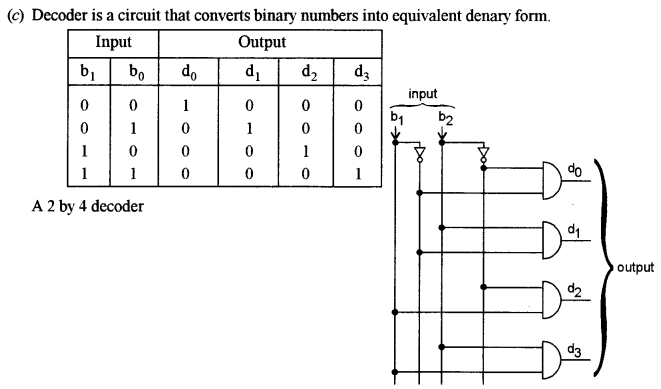
(c) What is a Decoder? Draw the truth table and logic circuit diagram for a 2 to 4 Decoder. [4]
Answer:
Question 7.
(a) What is Full Adder? Draw the truth table for a Full adder. Also, derive SOP expression for the Full Adder and draw its logic circuit. [4]
(b) State how a Decoder is different from a Multiplexer. Also, state one use of each. [3]
(c) Convert the following cardinal expression into its canonical form and reduce it using Boolean laws: [3]
F(L, M, O, P) = Π (0, 2, 8, 10)
Answer:
(a) A full adder is a logic circuit that can add three bits at a time producing two outputs one of which is the Sum bit and the other is Carry bit.

(b) A Multiplexer is a circuit that selects one of many input channels and connects it to the output channel. Whereas a decoder is a circuit tan converts binary numbers to denary numbers
A multiplexer is used as a common bus system. Whereas a decoder is used in converting binary to denary.
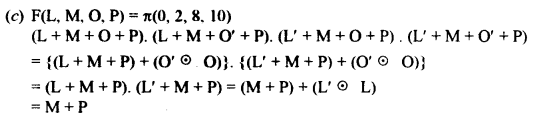
Section – B
Answer any two questions
- Each program should be has written in such a way that it clearly depicts the logic of the problem.
- This can be achieved by using mnemonic names and comments in the program.
- Flowcharts and Algorithms are not required
- The programs must be written in Java
Question 8.
Input a sentence from the user and count the number of times, the words “an” and “and” are present in the sentence. Design a class Frequency using the description given below: [ 10]
Class name: Frequency
Data members/variables:
text: stores the sentence
countand: to store the frequency of the word “and”
countan: to store the frequency of the word “an”
len: stores the length of the string
Member functions/methods:
Frequency(): constructor to initialize the instance variables
void accept(String n): to assign n to text, where the value of the parameter n should be in lower case.
void checkandfreq(): to count the frequency of “and”
void checkanfreq(): to count the frequency of “an”
void display(): to display the number of “and” and “an” with appropriate messages.
Specify the class Frequency giving details of the constructor(), void accepts(String), void checkandfreq(), void checkanfreq() and void display(). Also, define the main() function to create an object and call methods accordingly to enable the task.
Answer:
Class frequency
{
String text;
Public int countand;
Public int countan:
Public int len;
Frequency()
{
text = "countand = 0;
countan = 0:
len = 0;
}
void accept(String n)
{
n = text:
}
void check and freq()
{ String S = " "; countand = 0 ;
len = n. length();
for (int i = 0; i < len; i++)
{
char b = n. charAt(i);
if(b = = ' ')
{
if (S = = "and'')
{
countand = countand + 1;
}
S = " ";
}
else
S = S+b;
}
}
}
void checkanfreq()
{
String S1 = " ";
countan = 0;
len = n. length ( )
for (int i = 0; i < n; i++)
{
char b = n.charAt(i);
if (b = = ' ');
{
if (S1 == "an")
{
countan = countan + 1;
}
S1 = " ";
}
else
{
S1 = S1 +b;
}
}
}
void display()
{
System.out pri nl n(' 'Frequency of'and' in the sentence is'' + countand);
System.out.println(''Frequency of 'an' in the sentence is'' + countan);
}Question 9.
A class DeciOct has been defined to convert a decimal number into its equivalent octal number. Some of the members of the class are given below:
Class name: DeciOct
Data members/instance variables:
n: stores the decimal number
oct: stores the octal equivalent number
Member functions:
DeciOct(): constructor to initialize the data members
n = 0, oct = 0.
void getnum(int nn): assign nn to n
void deci_oct(): calculates the octal equivalent of ‘n’ and stores it in oct using the recursive technique
void show(): displays the decimal number ‘n’, calls the function deci_oct() and displays its octal equivalent.
(a) Specify the class DeciOct, giving details of the constructor( ), void getnum(int), void deci_oct( ) and void show(). Also define a main() function to create an object and call the functions accordingly to enable the task. [8]
(b) State any two disadvantages of using recursion. [2]
Answer:
(a) Class DeciOct
{
Public int n ;
Public int oct;
DeciOct()
{
n = 0;
Oct = 0;
}
void getnum.(int nn)
{
n = nn;
}
void deci_oct( )
{
int t = n;
int r = 0;
int s;
while (t! = 0)
{
s = t % 8;
r = 10 * r + s;
}
Oct = 0;
while (r! = 0)
{
int p = r% 10
Oct = 10 * Oct + p;
r = r/10;
}
}
void show( )
{
System.out.println ('' The decimal number is " + n);
System.out.println ("The octal of "+ n + " is" + oct);
}(b) The two disadvantages of recursion are:
(i) It takes more time to compile.
(ii) Much memory blocks are wasted.
(c) input java. io. *;
class abc
{
public static void main (String args [ ]) throws IO Exception
{
frequency ob = new frequency( );
BufferedReader B = new BufferedReader (new InputStream - Reader (System.in));
String p = B.readLine( )
Ob.accept(p);
Ob.checkandfreq( );
Ob.checkanfreq( );
Ob.display( );
}
}Question 10.
You are given a sequence of N integers, which are called as pseudo arithmetic sequences [10]
(sequences that are in arithmetic progression).
Sequence of N integers : 2, 5, 6, 8, 9, 12
We observe that 2 + 12 = 5 + 9 = 6 + 8 = 14
The sum of.the above sequence can be calculated as 14 × 3 = 42.
For sequence containing an odd number of elements the rule is to double the middle element,
for example 2, 5, 7, 9, 12 = 2 + 12 = 5 + 9 = 7 + 7 = 14.
14 × 3 = 42 [middle element = 7]
A class Pseudoarithmetic determines whether a given sequence is a pseudo-arithmetic sequence.
The details of the class are given below:
Class name: Pseudoarithmetic
Data members/instance variables:
n: to store the size of the sequence
a[]: integer array to store the sequence of numbers
ans, flag: store the status
sum: store the sum of the sequence of numbers
r: store the sum of the two numbers
Member functions:
Pseudoarithmetic(): default constructor
void accept(int nn): to assign nn to n and to create an integer array. Fill in the elements of the array
boolean check(): return true if the sequence is a pseudo arithmetic sequence otherwise returns false
Specify the class Pseudoarithmetic, giving the details of the constructor(), void accept(int) and boolean check(). Also, define a main() function to create an object and call the member functions accordingly to enable the task.
Answer:
import java.io. *
clas Pseudoarithmetic
{
Public int n;
Public int a [ ];
Public int ans;
Public int flag;
Public int sum;
Public int r;
Pseudoarithmetic()
{
n = 0; flag = 0; sum = 0;
}
void accept(int nn)
{
n = nn;
BufferedReader B = new BufferedReaderf new InputStreamReader (System, in));
a [n];
(int i = 0; i < n; i++)
{
a [i] = Integer.parselnt (B.readLine( ));
sum = sum + a[i];
}
}
boolean check( )
{
if(n%2 = = 0)
{ int i = 0;p = n-1;
while (i < p)
{
r = a[i] + a[p]
if (r == (a [i + 1] + a [p - 1] && (r*3) = = sum)
{
flag = 0;
}
p = p-1;i = i + 1;
else
else if (n%2 ! = 0)
{
int i = 0;p = n-1;
while (i <=p)
{
r=a[i] + a[p]
if (r== (a [i +1] + a[p -1]) && (r*3) = = sum)
{
flag = 0;
}
else
{
flag= 1;
}
p = p-1;i = i+1;
}
}
if(flag = = 0)
return true;
else
return false;
}Section – C
Answer any two questions
- Each Program /Algorithm should be written in such a way that it clearly depicts the logic of the problem stepwise.
- This can also be achieved by using pseudo-codes.
- Flowcharts are not required
- The programs must be written in Java.
- The Algorithm must be written in general/standard form.
Question 11.
A superclass Record has been defined to store the names and ranks of 50 students. Define a sub-class Rank to find the highest rank along with the name. The details of both classes are given below: [10]
Class name: Record
Data members/instance variables:
name[]: to store the names of students
mk[]: to store the ranks of students
Member functions:
Record(): constructor to initialize data members
void readvalues(): to store the names and ranks
void display(): displays the names and the corresponding ranks
Class name: Rank
Data members/instance variables:
index: integer to store the index of the topmost rank
Member functions:
Rank(): constructor to invoke the base class constructor and to initialize index = 0
void highest(): finds the index/location of the topmost rank and stores it in the index without sorting the array.
void display(): displays the names and rank along with the name haring the topmost rank.
Specific the class Record giving details of the constructor(), void readvalues( ) and void display (). Using the concept of inheritance, specify the class Rank giving details of constructor ( ), void highest() and void display().
THE MAIN() FUNCTION AND ALGORITHM NEED NOT BE WRITTEN.
Answer:
import java. io. *;
Class Record
{
Public String name [50];
Public int rank [50];
Record()
{
name[] = { };
mk[] = { };
}
void readvalues( )
{
BufferedReader B = new BuiferedReader (new InputStieamReader(systeni.in));
for (int i = 0; i < 50; i++)
{
System.out.println("Enter name and corresponding rank);
name[i| = B.readLine( );
mk[i] = Integer.parselnt (B.readLine());
}
voiddisplay( )
{
System.out.println("The names and corresponding ranks are : ");
for(int i = 0; i < 50; i++)
{
System.out.println(name[i] +" ''+mk[i]);
}
}
Class Rank extends Record
{
Public int index;
Rank( )
{
super.Record( );
index=0;
}
void highest()
{
index;
int a = 0;
for(int i = 0; i < 50; i++)
{
for(int j = 0; j < 50; j++)
{
if (mk [i] < mk [j])
{
index = i;
}
}
}
}
void display()
{
Super.display( );
System.out.println ("The Topmost rank activer is " + name [index] + " "+ mk [index]); .
}Question 12.
A stack is a kind of data structure which can store elements with the restriction that an element can be added or removed from the top only.
The details of the class Stack is given below:
Class name: Stack
Data members/instance variables:
st[]: the array to hold the names
size: the maximum capacity of the string array
top: the index of the topmost element of the stack
ctr: to count the number of elements of the stack
Member functions:
Stack( ): default constructor
Stack(int cap): constructor to initialize size = cap and top = -1
void pushname(String n): to push a name onto the stack. If the stack is full, display the message “OVERFLOW”
String popname(): removes a name from the top of the stack and returns it. If the stack is empty, display the message “UNDERFLOW”
void display(): Display the elements of the stack.
(a) Specify class Stack giving details of the constructors(), void pushname(String n), String popname() and void display(). [8]
THE MAIN() FUNCTION AND ALGORITHM NEED NOT BE WRITTEN.
(b) Under what Principle does the above entity work?
Answer:
(a) Class Stack
{
String ST [ ];
int size;
int top;
int etr;
Stack( )
{
for(int i = 0; i <10; i++)
St [i] = " ";
size = 0;
top = 0;
ctr = 0;
Stack(int cap)
{
size = cap
St [size];
top = -1 ;
void pushname (String n)
{
if (top = = (size - 1))
System.out.println (''overflow'');
else
{
top ++;
St [top] = n;
}
}
String popname( )
{
String v;
if(top = = -1)
System.out.println(''underflow ");
else
{
v = St[top];
System.out.println("poped element is''+'' : " + v);
top--;
}
}
void display
{
if(top == -1)
System.out.println(''empty'');
else
{
for (int i = top-1; i > = 0 ; i--)
{
System.out.println(St [i]):
}
}
}(b) Stack works on LIFO (Lost In First Out) principle.
Question 13.
(a) A linked list is formed from the objects of the class, [4]
class Node
{
into info;
Node link;
}Write an algorithm OR a Method for deleting a node from a linked list.
The method declaration is given below :
void delete node (Node start)
(b) Distinguish between worst-case and best-case complexity of an algorithm. [2]
(c) Answer the following from the diagram of a Binary Tree given below:
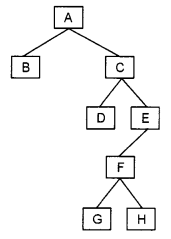
(i) Write the Postorder tree traversal. [1]
(ii) Name the Leaves of the tree. [1]
(iii) Height of the tree. [1]
(iv) Root of the tree. [1]
Answer:
(a) Algorithm
(i) Copy the content of the next mode into the mode that has to be deleted.
(ii) Assign the next pointer of the newly copied node of the next pointer of the node from the content has been copied.
(iii) Delete the node from the data has copied.
(b) Best case scenario for an algorithm is the arrangement of data for which the algorithm performs the best, eg., binary search.
The worst-case scenario, on the other hand, describes the absolute worst set of input for a given algorithm, e.g., quicksort.
(c) (i) B D G H F E C A
(ii) B, D, G, H
(iii) 5
(iv) A
