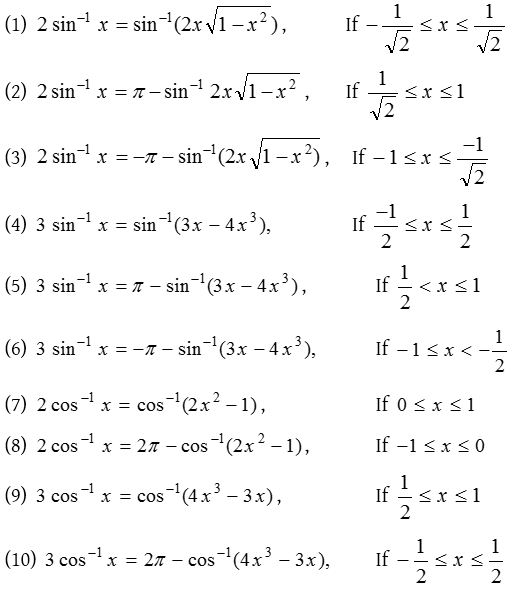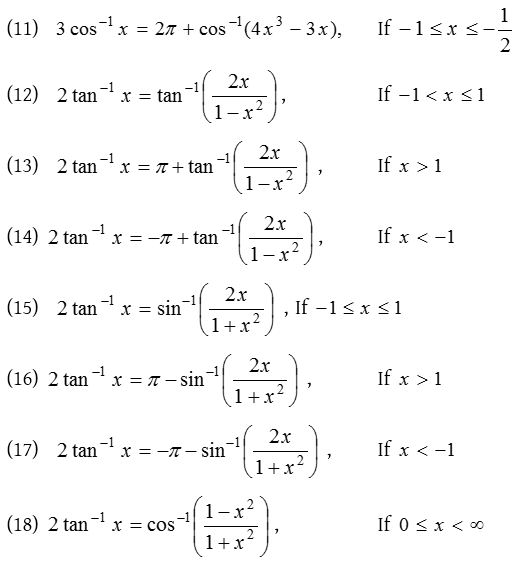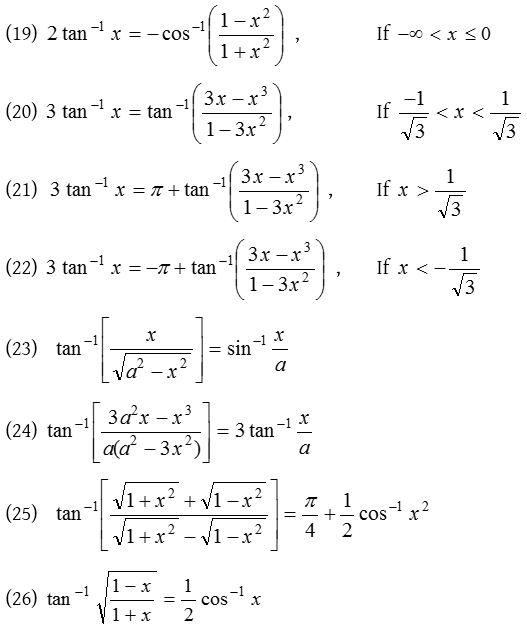What are the Inverse Trigonometric Functions?
The inverse of a function f : A → B exists if f is one-one onto i.e., a bijection and is given by f(x) = y ⇒ f-1(y) = x.
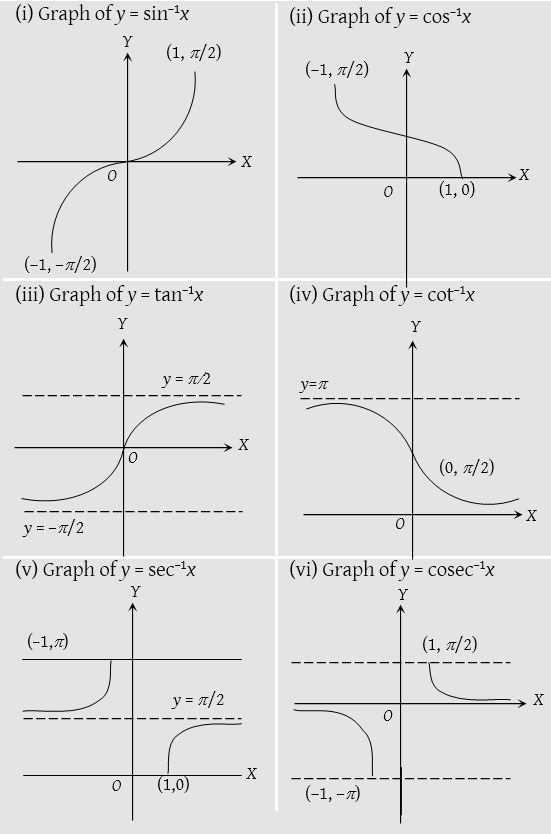
Graphs of inverse trigonometric functions
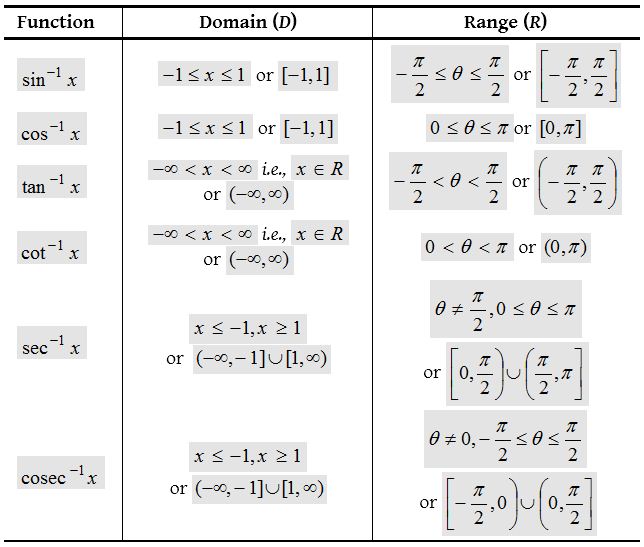
Domain and Range of inverse trigonometric functions
Properties of inverse trigonometric functions

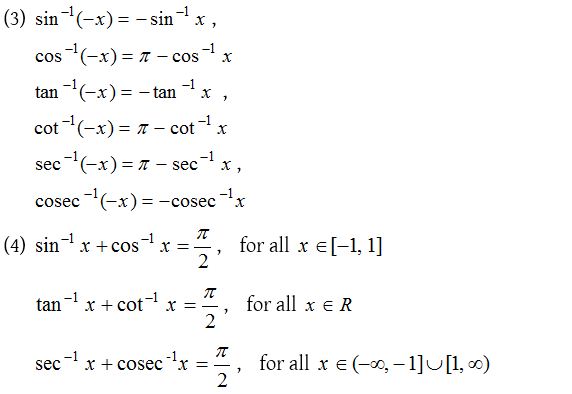
(5) Principal values for inverse circular functions:

(6) Conversion property:
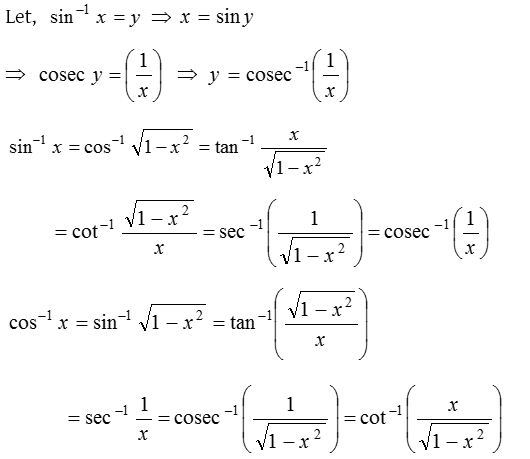
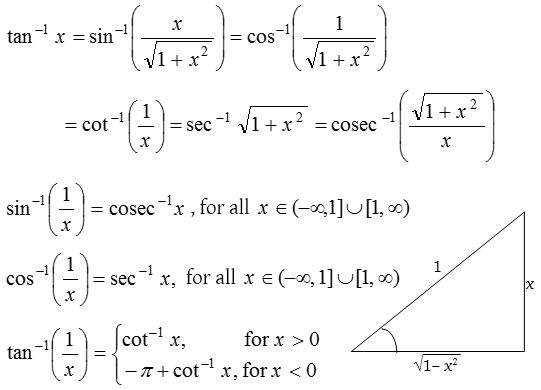
(7) General values of inverse circular functions:
We know that if ? is the smallest angle whose sine is x, then all the angles whose sine is x can be written as nx + (−1)n? where n = 0, 1, 2, ……. Therefore, the general value of sin−1 x can be taken as nx + (−1)n?. The general value of sin−1 x is denoted by sin−1 x.
Thus, we have
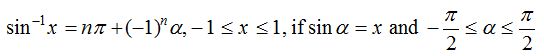
Similarly, general values of other inverse circular functions are given as follows:
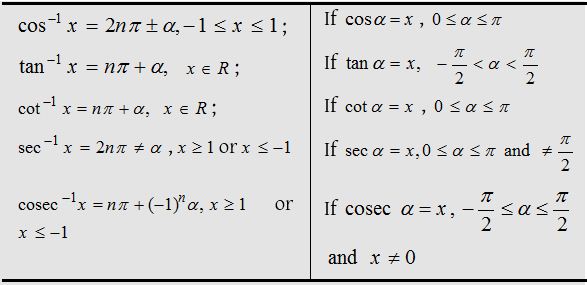
Formulae for sum, difference of inverse trigonometric function
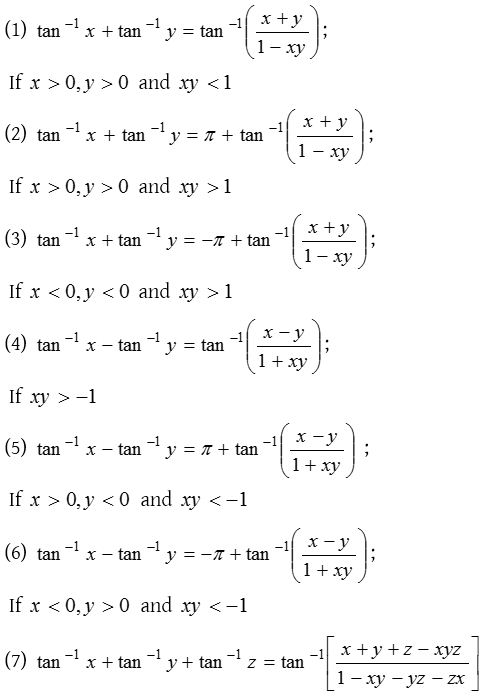
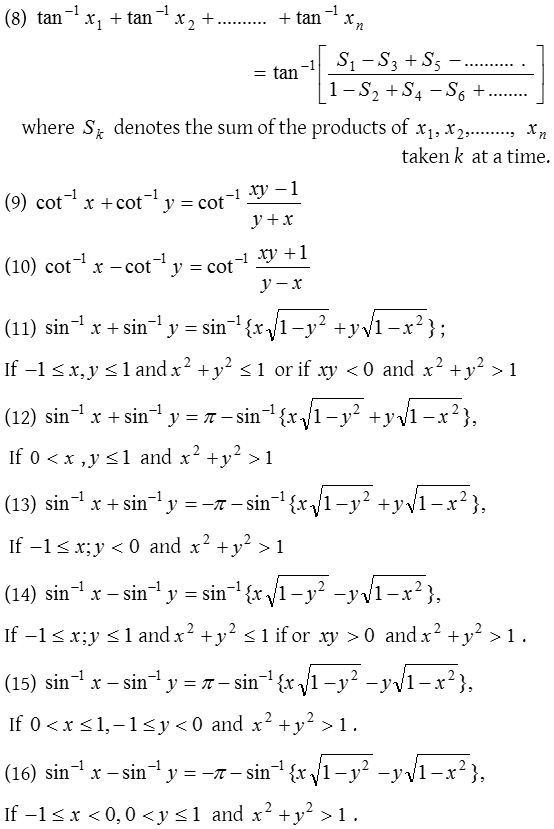
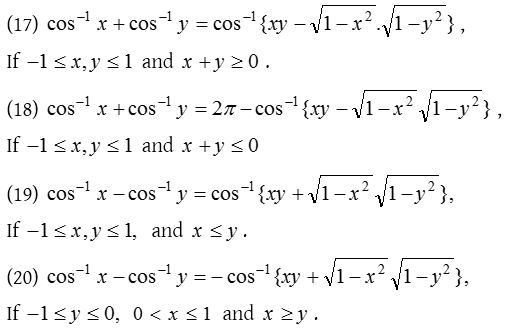
Inverse trigonometric ratios of multiple angles