Intuitive Notion of Line Symmetry and Plane Symmetry
Line symmetry
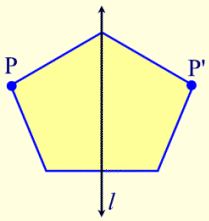
Line symmetry, or just symmetry, occurs when two halves of a figure mirror each other across a line. The line of symmetry is the line that divides the figure into two mirror images. A simple test to determine if a figure has line symmetry is to fold the figure along the supposed line of symmetry and see if the two halves of the figure coincide.
A figure in the plane has a line of symmetry if the figure can be mapped onto itself by a reflection in the line.
- Nature displays line symmetry in some of its most beautiful work. The balanced arrangement of symmetry creates pleasing and attractive forms.
 The white line is the line of symmetry.
The white line is the line of symmetry. - Many flowers possess line symmetry. The biologist’s term for line symmetry is “bilateral symmetry.”
 The black lines are the line of symmetry.
The black lines are the line of symmetry. - Mosaics and art work often demonstrate the concept of reflections and line symmetry. This drawing has two lines of symmetry, as shown by the white lines.

- This butterfly caterpillar displays line symmetry.
 The pink line is the line of symmetry.
The pink line is the line of symmetry. - Certain letters of the alphabet and words possess line symmetry (such as the samples in the photo).
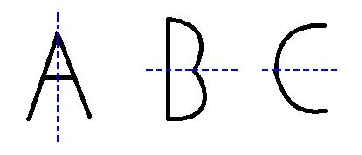 Notice that some letters possess vertical line symmetry, some possess horizontal line symmetry, and some possess BOTH vertical and horizontal line symmetry.
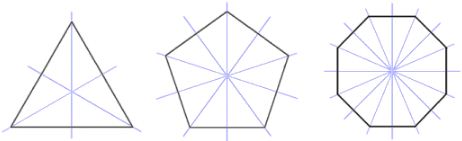
Notice that some letters possess vertical line symmetry, some possess horizontal line symmetry, and some possess BOTH vertical and horizontal line symmetry. - Certain geometric figures possess line symmetry. The figures in the photo are only a sampling of the geometric figures which possess symmetry.
Plane symmetry
Plane symmetry occurs when a plane intersects a three dimensional figure such that one half is the reflected image of the other half. Such a plane is imaginary and divides an object into two halves, each of which is the mirror image of the other in this plane.
Plane symmetry is analogous to line symmetry, only in three dimensions. Common objects displaying plane symmetry are rectangular solids, spheres, boxes, cones, and humans.


Doctors repair damaged human faces by reconstructing the symmetry plane of the former healthy face from the damaged asymmetrical patient’s face.
Definition: A set of points has line symmetry if and only if there is a line, l, such that the reflection through l of each point of the set is also a point of the set.