Injective, Surjective and Bijective

Injective, Surjective and Bijective

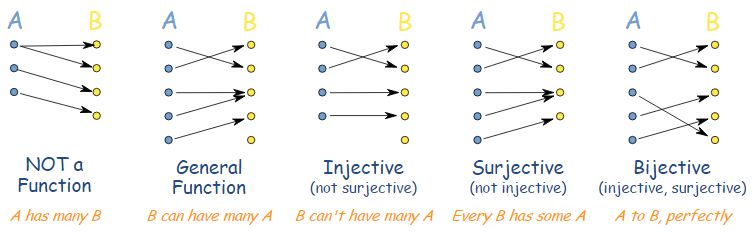
One-one function (Injection)

A function f : A ⟶ B is said to be a one-one function or an injection, if different elements of A have different images in B. Thus, f : A ⟶ B is one-one.
a ≠ b ⇒ f(a) ≠ f(b) for all a, b ∈ A
⟺ f(a) = f(b) ⇒ a = b for all a, b ∈ A.
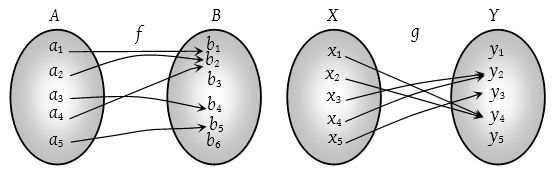
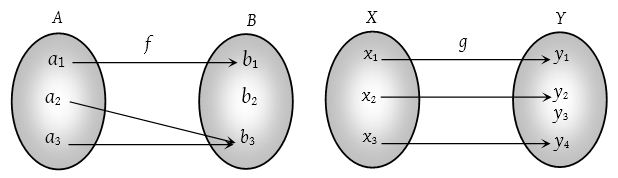
e.g. Let f : A ⟶ B and g : X ⟶ Y be two functions represented by the following diagrams.

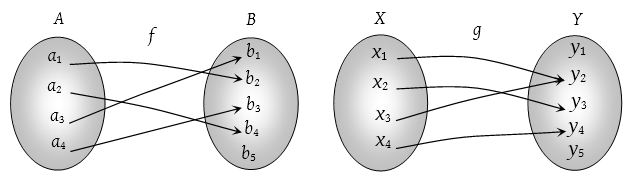
Clearly, f : A ⟶ B is a one-one function. But g : X ⟶ Y is not one-one function because two distinct elements x₁ and x₃ have the same image under function g.

(i) Method to check the injectivity of a function:
Step I: Take two arbitrary elements x, y (say) in the domain of f.
Step II: Put f(x) = f(y).
Step III: Solve f(x) = f(y) If f(x) = f(y) gives x = y only, then f : A ⟶ B is a one-one function (or an injection). Otherwise not.
If function is given in the form of ordered pairs and if two ordered pairs do not have same second element then function is one-one.
If the graph of the function y = f(x) is given and each line parallel to x-axis cuts the given curve at maximum one point then function is one-one. e.g.

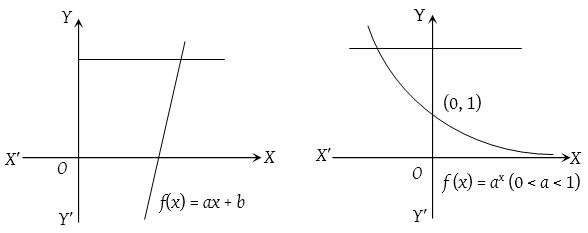
(ii) Number of one-one functions (Injections):
If A and B are finite sets having m and n elements respectively, then number of one-one functions from

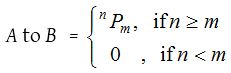
Many-one function

A function f : A ⟶ B is said to be a many-one function if two or more elements of set A have the same image in B.
Thus, f : A ⟶ B is a many-one function if there exist x, y ∈ A such that x ≠ y but f(x) = f(y).
In other words, f : A ⟶ B is a many-one function if it is not a one-one function.

• If function is given in the form of set of ordered pairs and the second element of atleast two ordered pairs are same then function is many-one.
• If the graph y = f(x) of is given and the line parallel to x-axis cuts the curve at more than one point then function is many-one.
  

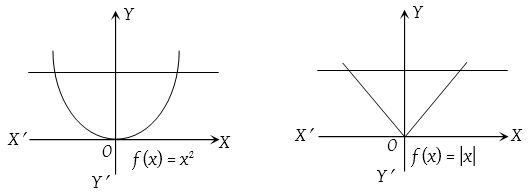
Onto function (Surjection)

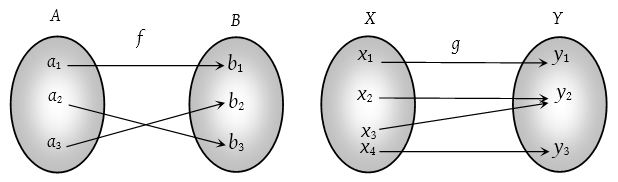
A function f : A ⟶ B is onto if each element of B has its pre-image in A. Therefore, if f^-1(y) ∈ A, ∀ y ∈ B then function is onto. In other words, Range of f = Co-domain of f. e.g. The following arrow-diagram shows onto function.

Number of onto function (Surjection):
If A and B are two sets having m and n elements respectively such that 1 ≤ n ≤ m then number of onto functions from

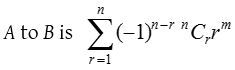
Into function

A function f : A ⟶ B is an into function if there exists an element in B having no pre-image in A.
In other words, f : A ⟶ B is an into function if it is not an onto function e.g. The following arrow-diagram shows into function.

(i) Method to find onto or into function:
(a) Solve f(x) = y by taking x as a function of y i.e., g(y) (say).
(b) Now if g(y) is defined for each y ∈ co-domain and g(y) ∈ domain for y ∈ co-domain, then f(x) is onto and if any one of the above requirements is not fulfilled, then f(x) is into.

One-one onto function (Bijection)

A function f : A ⟶ B is a bijection if it is one-one as well as onto.
In other words, a function f : A ⟶ B is a bijection if

1. It is one-one i.e., f(x) = f(y) ⇒ x = y for all x, y ∈ A.
2. It is onto i.e., for all y ∈ B, there exists x ∈ A such that f(x) = y.

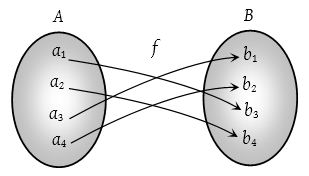
Clearly, f is a bijection since it is both injective as well as surjective.

Number of one-one onto function (bijection):
If A and B are finite sets and f : A ⟶ B is a bijection, then A and B have the same number of elements. If A has n elements, then the number of bijection from A to B is the total number of arrangements of n items taken all at a time i.e. n!.