ICSE Maths Previous Year Question Paper 2016 Solved for Class 10
ICSE Paper 2016
MATHEMATICS
(Two hours and a half)
Answers to this Paper must be written on the paper provided separately.
You will not be allowed to write during the first 15 minutes.
This time is to be spent in reading the question paper.
The time given at the head of this Paper is the time allowed for writing the answers.
Attempt all questions from Section A and any four questions from Section B.
All working, including rough work, must be clearly shown and must be done on the same sheet as the rest of the answer. Omission of essential working will result in the loss of marks.
The intended marks for questions or parts of questions are given in brackets [ ].
Mathematical tables are provided.
SECTION A [40 Marks]
(Answer all questions from this Section.)
Question 1:
(a) Using remainder theorem, find the value ofk if on dividing 2x3 + 3x2 – kx + 5 by x-2, leaves a remainder 7. [3]
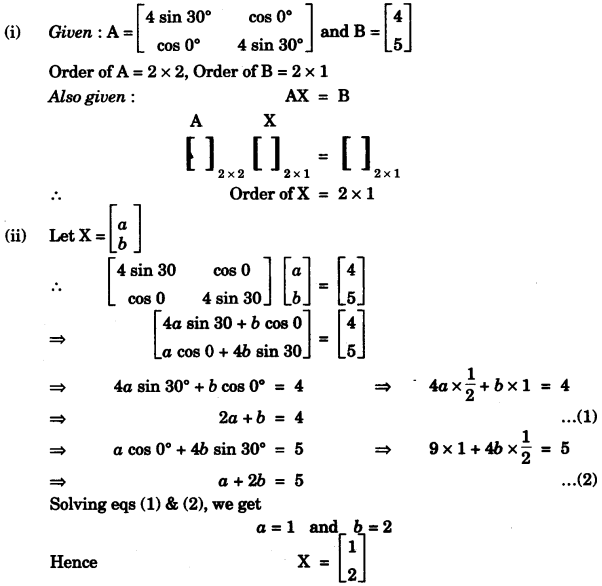
(b) Given A = [20−17] and I = [1001] and A2=9A+mI. Find m. [4]
(c) The mean of following numbers is 68. Find the value of ‘x’: 45, 52, 60, x, 69, 70, 26, 81 and 94. Hence estimate the median. [3]
Solution:
(a)

(b)
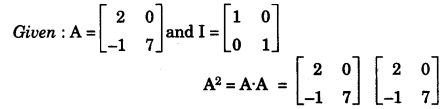

(c)

Question 2:
(a) The slope of a line joining P(6, k) and Q(1 – 3k, 3) is 12. Find : [3]
(i) k
(ii) Midpoint of PQ, using the value of ‘k’ found in (i).
(b) Without using trigonometrical tables, evaluate :
cosec2 57° – tan2 33° + cos 44° cosec 46° – √2 cos 45° – tan2 60° [4]
(c) A certain number of metallic cones, each of radius 2 cm and height 3 cm are melted and recast into a solid sphere of radius 6 cm. Find the number of cones. [3]
Solution:
(a) (i)
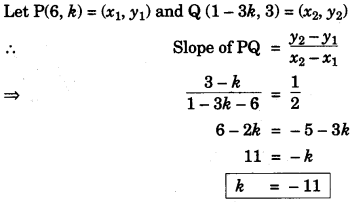
(ii)
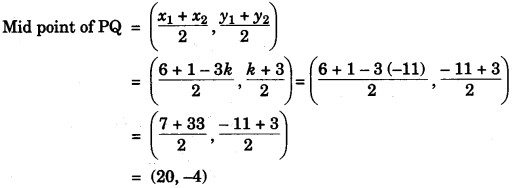
(b)
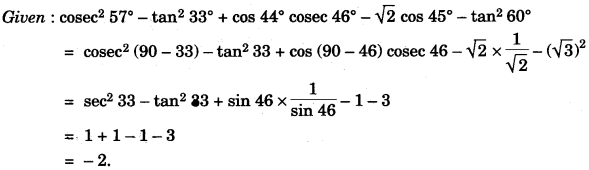
(c)
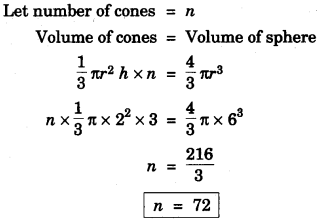
Question 3:
(a) Solve the following inequation, write the solution set and represent it on the number line. [3]
![]()
(b) In the given figure below, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
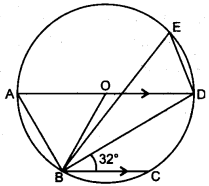
Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED [4]
(c) If (3a + 2b) : (5a + 3b) = 18 : 29. Find a : b. [3]
Solution:
(a)

(b)
(c)
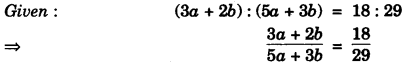

Question 4:
(a) A game of number has cards marked with 11, 12, 13, 40. A card is drawn at random. Find the Probability that the number on the card drawn is :
(i) A perfect square
(ii) Divisible by 7. [3]
(b) Use graph paper for this question.
(Take 2 cm = 1 unit along both x and y axis).
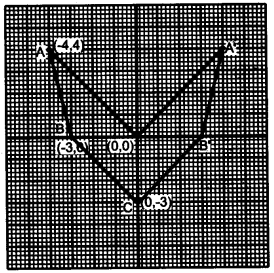
Plot the point O (0, 0), A (-4, 4), B (-3, 0) and C (0, -3).
(i) Reflect points A and B on the y axis and name them A’and B’respectively. Write down their coordinates.
(ii) Name the figure OABCB’A’.
(iii) State the line of symmetry of this figure. [4]
(c) Mr. Lalit invested Rs. 5,000 at a certain rate of interest, compounded annually for two years. At the end of first year it amounts to Rs. 5,325. Calculate :
(i) The rate of interest.
(ii) The amount at the end of second year, to the nearest rupee. [3]
Solution:
(a) Total number of all possible outcomes = 30.

(b) (i) A'(4,4) and B'(3, 0)
(ii) Arrow Head
(iii) y-axis is the line of symmetry.
 (c) Given : Principal = Rs. 5,000, Time = 2 years, After one year amount = Rs. 5,325
(c) Given : Principal = Rs. 5,000, Time = 2 years, After one year amount = Rs. 5,325


SECTION B [40 Marks]
Answer any four Questions in this Section.
Question 5:
(a) Solve the quadratic equation x2 – 3(x + 3) = 0; Give your answer correct to two significant figures. [3]
(b) A page from the saving bank account of Mrs. Ravi is given below :
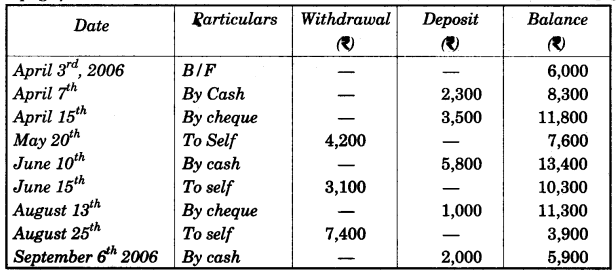
She closed the account on 30th September, 2006. Calculate the interest Mrs. Ravi earned at the end of 30th September, 2006 at 4.5% per annum interest. Hence find the amount she receives on closing the account. [4]
(c) In what time will Rs. 1500 yield Rs. 1996.50 as compound interest at 15% per annum compounded annually ? [3]
Solution:
(a) Given:
x2 – 3 (x +3) = 0
x2 – 3x – 9 = 0
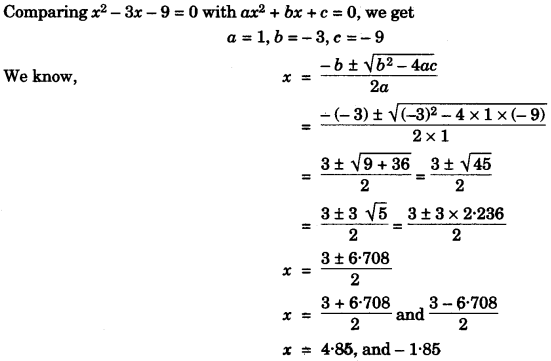
(b) For interest as per the entries of the pasbook, we have
| Month | Minimum balance between 10th day and the last day (in Rs.) |
| April | 8,300 |
| May | 7,600 |
| June | 10,300 |
| July | 10,300 |
| August | 3,900 |
| Total % | 40,400 |

(c)
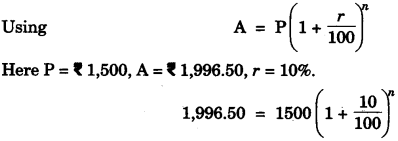
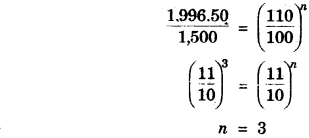
Question 6:
(a) Construct a regular hexagon of side 5 cm. Hence construct all its lines of symmetry and name them. [3]
(b) In the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T. [4]
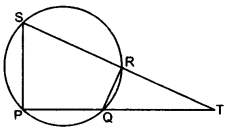
(i) Prove ∆ TPS ~ ∆ TRQ.
(ii) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm.
(iii) Find area of quadrilateral PQRS if area of ∆ PTS = 27cm2.
Solution:
(a) Steps of Construction:
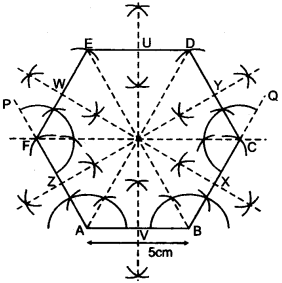
(i) Using the given data, construct the regular hexagon ABCDEF with each side equal to 5 cm.
(ii) Draw the perpendicular bisectors of sides AB, BC, CD, DE, EF and FA which intersect AB at V, BC at X, CD at Y, DE at U, EF at W and FA at Z.
(iii) Join the mid points of opposite sides i.e., UV, WX and YZ and the diagonals passing through the centres i.e., AD, BE and CF.
Hence A regular hexagon has six lines of symmetry – UV, WX, YZ, AD, BE, CF.
(b)

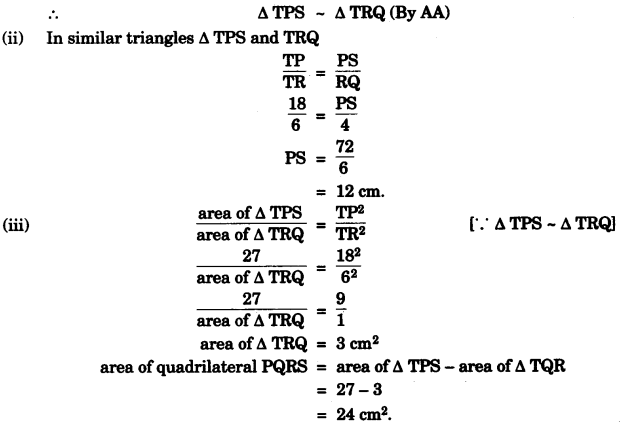
(c)
Question 7:
(a) An aeroplane at an altitude of 1500 metres finds that two ships are sailing towards it in the same direction. The angles of depression as observed from the aeroplane are 45° and 30° respectively. Find the distance between the two ships. [4]
(b) The table shows the distribution of the scores obtained by 160 shooters in a shooting competition. Use a graph sheet and draw an ogive for the distribution.
(Take 2 cm = 10 scores on the X axis and 2 cm = 20 shooters on the Y-axis).
| Scores | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No. of shooters | 9 | 13 | 20 | 26 | 30 | 22 | 15 | 10 | 8 | 7 |
Use your graph to estimate the following:
(i) The median.
(ii) The interquartile range.
(iii) The number of shooters who obtained a score of more than 85%. [6]
Solution:
(a)
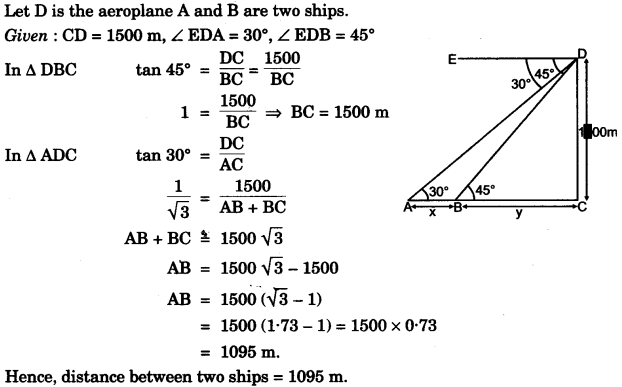
(b)
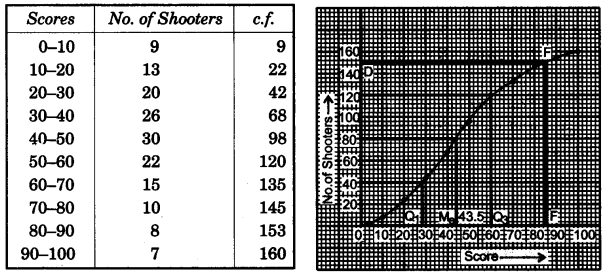

(iii) The number of shooter who obtained a score of more 85%, from E draw a vertical line to meet ogive at F. From F draw a horizontal line to D.
= 160 – 150 = 10
Question 8:
![]()
(b) Draw a line AB = 5 cm. Mark a point C on AB such that AC = 3 cm. Using a ruler and a compass only, construct: [4]
(i) A circle of radius 2.5 cm, passing through A and C.
(ii) Construct two tangents to the circle from the external point B. Measure and record the length of the tangents.
(c) A line AB meets X-axis at A and Y-axis at B. P(4, -1) divides AB in the ratio 1:2.
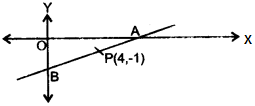
(i) Find the coordinates of A and B.
(ii) Find the equation of the line through P and perpendicular to AB. [3]
Solution:
(a)
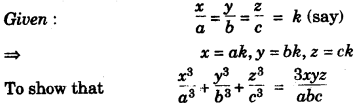
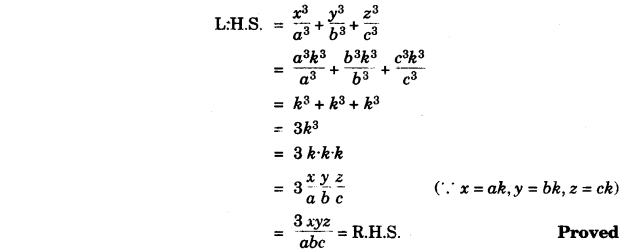
(b) Steps of Construction:
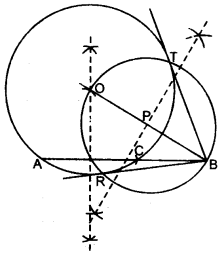
(i) (1) Draw line AB = 5 cm
(2) From AB cut AC = 3 cm.
(3) Draw right bisector of AC.
(4) Taking A as centre and AO = 2.5 cm cm as radius, draw an arc to meet the right bisector of AC at O.
(5) Taking O as the centre and AO = 2.5 cm as radius, draw a circle, which passing through A&C.
(6) Join BO.
(7) Draw right bisector of BO, which cuts BO at P.
(8) Taking P as centre and OP as radius, draw a circle which cuts old circle at R & T.
(9) Join BR and BT.
These are required tangents.
(ii) Length of tangent = 3 cm.
(c)


Question 9:
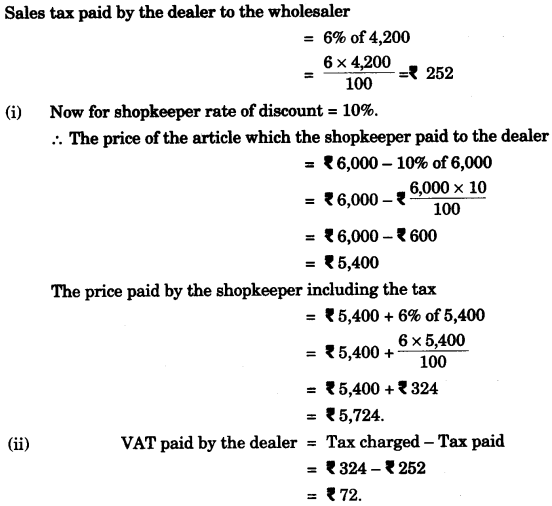
(a) A dealer buys an article at a discount of 30% from the wholesaler, the marked price being ? 6,000. The dealer sells it to a shopkeeper at a discount of 10% on the marked price. If the rate of VAT is 6%, find:
(i) The price paid by the shopkeeper including the tax.
(ii) The VAT paid by the dealer. [3]
(b) The given figure represents a kite with a circular and a semicircular motifs stuck on it. The radius of circle is 2.5 cm and the semicircle is 2 cm. If diagonals AC and BD are the lengths 12 cm and 8 cm respectively, find the area of the :
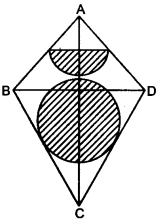
(i) shaded part. Give your answer correct to the nearest whole number.
(ii) unshaded part. [4]
(c) A model of a ship is made to a scale 1 : 300.
(i) The length of the model of the ship is 2 m. Calculate the length of the ship.
(ii) The area of the deck ship is 180,000 m2. Calculate the area of the deck of the model.
(iii) The volume of the model is 6.5 m3. Calculate the volume of the ship. [3]
Solution:
(a)

(b)

= 22 square cm
(c)

Question 10:
(a) Mohan has a recurring deposit account in a bank for 2 years at 6% p.a. simple interest. If he gets ? 1200 as interest at the time of maturity, find :
(i) the monthly installment.
(ii) the amount of maturity. [3]
(b) The histogram below represents the scores obtained by 25 students in a Mathematics mental test. Use the data to :
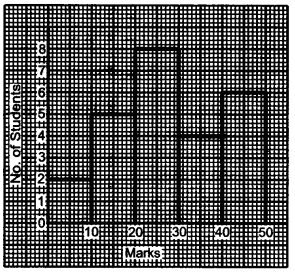
(i) Frame a frequency distribution table.
(ii) To calculate mean.
(iii) To determine the Modal class. [4]
(c) A bus covers a distance of 240 km at a uniform speed. Due to heavy rain its speed gets reduced by 10 km/h and as such it takes two hrs longer to cover the total distance. Assuming the uniform speed to be ‘x”km/h, form an equation and solve it to evaluate ‘x’. [3]
Solution:
(a)

(b) (i) Frequency distribution table :
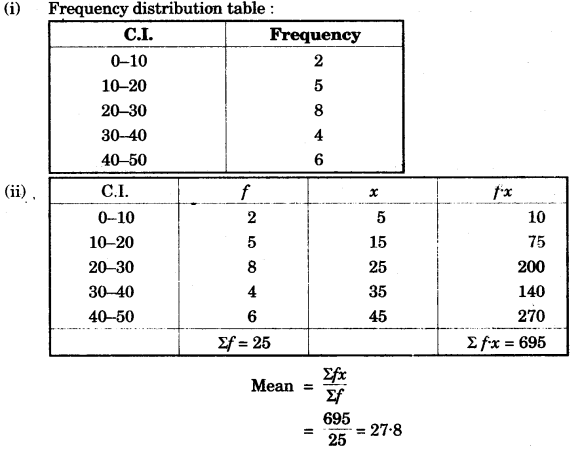
(iii) Model class = 20-30
(c)


Question 11:
![]()
(b) Use ruler and compasses only for the following question. All construction lines and arcs must he clearly shown. [4]
(i) Construct a A ABC in which BC = 6.5 cm, ∠ABC = 60°, AB = 5 cm.
(ii) Construct the locus of points at a distance of 3.5 cm from A.
(iii) Construct the locus of points equidistant from AC and BC.
(iv) Mark 2 points X and Y which are at a distance of 3.5 cm from A and also equidistant from AC and BC. Measure XY.
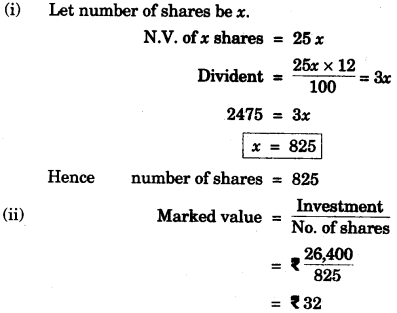
(c) Ashok invested f 26,400 on 12%, f 25 shares of a company. If he receives a dividend off. 2,475, find the:
(i) number of shares he bought.
(ii) Market value of each share. [3]
Solution:
(a)
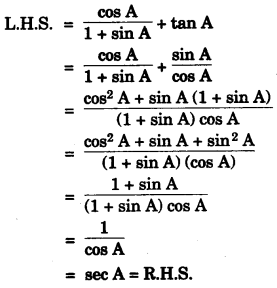
(b)
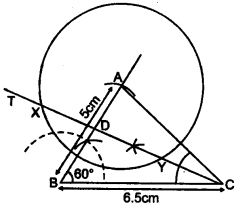
(i) Construct ∆ ABC with the given data.
(ii) Taking A as centre and radius is 3-5, draw a circle. Which is required locus.
(iii) Draw a angle bisector of C. Which is required locus.
(iv) Angle bisector of C cut above circle at two points i.e., X & Y.
These points are required points.
Length of XY = 5 cm.
(c)