ICSE Maths Previous Year Question Paper 2015 Solved for Class 10
ICSE Paper 2015
MATHEMATICS
(Two hours and a half)
Answers to this Paper must be written on the paper provided separately.
You will not be allowed to write during the first 15 minutes.
This time is to be spent in reading the question paper.
The time given at the head of this Paper is the time allowed for writing the answers.
Attempt all questions from Section A and any four questions from Section B.
All working, including rough work, must be clearly shown and must be done on the same sheet as the rest of the answer. Omission of essential working will result in the loss of marks.
The intended marks for questions or parts of questions are given in brackets [ ].
Mathematical tables are provided.
SECTION A [40 Marks]
(Answer all questions from this Section.)
Question 1:
(a) A shopkeeper bought an article for Rs. 3,450. He marks the price of the article 16% above the cost price. The rate of sales tax charged on the article is 10%. Find the :
(i) marked price of the article.
(ii) price paid by a customer who buys the article. [3]
(b) Solve the following inequation and write the solution set:
13x – 5 < 15x + 4 < 7x + 12, x ε R
Represent the solution on a real number line. [3]
(c) Without using trigonometric tables evaluate: [4]
![]()
Solution:
(a)
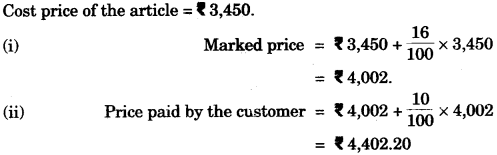
(b)
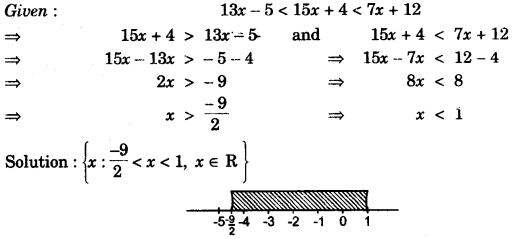
(c)

Question 2:
(a) If A = [3x01] and [9160−y], , find x and y when A2 = B.
(b) The present population of a town is 2,00,000. Its population increases by 10% in the first year and 15% in the second year. Find the population of the town at the end of the two years. [3]
(c) Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2) find:
(i) the coordinates of the fourth vertex D.
(ii) length of diagonal BD.
(iii) equation of side AB of the parallelogram ABCD. [4]
Solution:
(a)
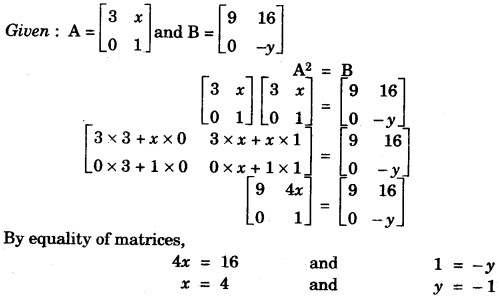
(b)
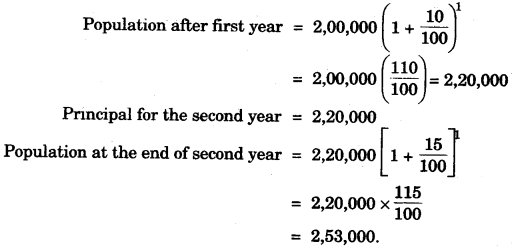
(c) Let the coordinate of D be (x, y). In a parallelogram, mid point of diagonal AC co-incides with the mid-point of diagonal BD.
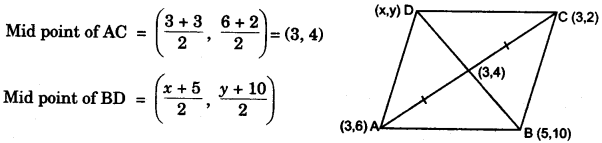

Question 3:
(a) In the given figure, ABCD is a square of side 21 cm. AC and BD are two diagonals of the square. Two semi circles are drawn with AD and BC as diameters. Find the areq of the shaded region.
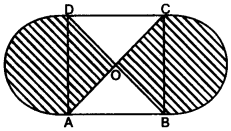
(Take π = 227 ). [3]
(b) The marks obtained by 30 students in a class assessment of 5 martks is given below: [3]
| Marks | 0 | 1 | 2 | 3 | 4 | 5 |
| No. of Students | 1 | 3 | 6 | 10 | 5 | 5 |
Calculate the mean, median and mode of the above distribution.
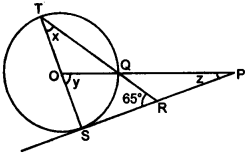
(c) In the figure given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and z. [4]
Solution:
(a) Given : Side = 21 cm,
Let Diagonal of the square = √2 (side)

(b)
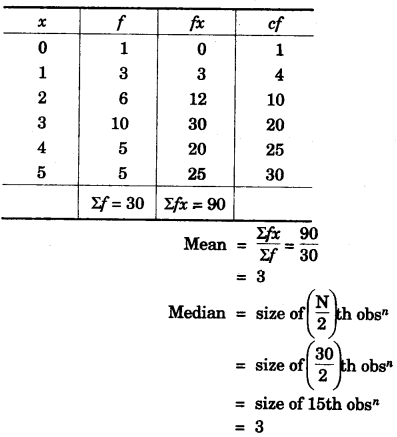
Mode = 3 marks (as highest frequency is 10)
(c)
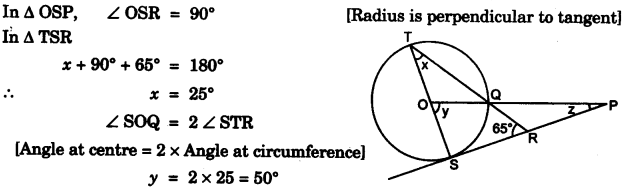
In ∆ OSP,
50° + 90° +z = 180°
∴ z = 40°
Question 4:
(a) Katrina opened a recurring deposit account with a Nationalised Bank for a period of 2 years. If the hank pays interest at the rate of 6% per annum and the monthly installment is 1,000, find the:
(i) interest earned in 2 years.
(ii) matured value. [3]
(b) Find the value of ‘K’ for which x = 3 is a solution of the quadratic equation, (K + 2) x2 – Kx + 6 = 0.
Thus find the other root of the equation. [3]
(c) Construct a regular hexagon of side 5 cm. Construct a circle circumscribing the hexagon. All traces of construction must be clearly shown. [4]
Solution:
(a)

(b)
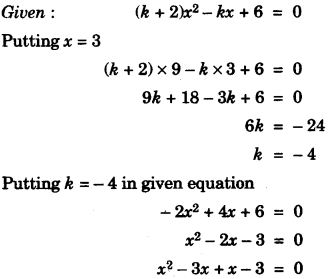
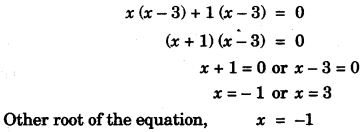
(c) Steps of Construction:
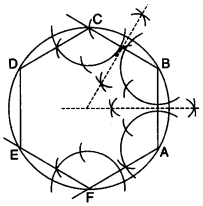
(i) Using the given data, construct the regular hexagon ABCDEF with each side equal to 5 cm.
(ii) Draw the perpendicular bisectors of sides AB and AF which intersect each other at point O.
(iii) With O as centre and OA as radius draw a circle which will pass through all the vertices of the regular hexagon ABCDEF.
SECTION B [40 Marks]
Answer any four Questions in this Section.
Question 5:
(a) Use a graph paper for this question taking 1 cm = 1 unit along both the x and y axis :
(i) Plot the points A(0, 5), B(2, 5), C(5, 2), D(5, -2), E(2, -5) and F(0, -5).
(ii) Reflect the points B, C, D and E on the y-axis and name them respectively as B’, C’, D’and E’
(iii) Write the coordinates of B’, C’, D’and E’.
(iv) Name the figure formed by BCDE E’D’CR’.
(v) Name a line of symmetry for the figure formed. [5]
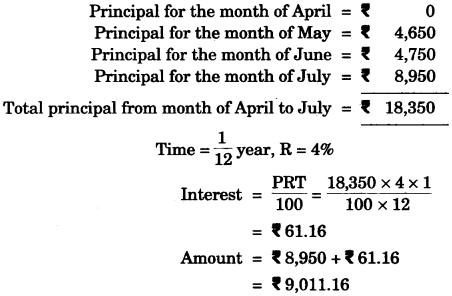
(b) Virat opened a Saving Bank account in a bank on 16th April 2010. His pass book shows the following entries:
| Date | Particulars | Withdrawal (Rs) | Deposit (Rs) | Balance (Rs) |
| April 16, 2010 | By cash | — | 2500 | 2500 |
| April 28th | By cheque | — | 3000 | 5500 |
| May 9th | To cheque | 850 | — | 4650 |
| May 15th | By cash | — | 1600 | 6250 |
| May 24th | To cash | 1000 | — | 5250 |
| June 4th | To cash | 500 | — | 4750 |
| June 30th | By cheque | — | 2400 | 7150 |
| July 3rd | By cash | — | 1800 | 8950 |
Calculate the interest Virat earned at the end of 31st July, 2010 at 4% per annum interest. What sum of money will he receive if he closes the account on 1st August, 2010 ? [5]
Solution:
(a) (i) See diagram below.
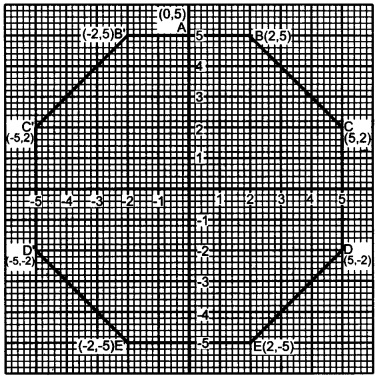
(ii) Coordinates:
B’ (-2, 5), C’ (-5, 2),
D’ (-5, -2), E’ (-2, -5)
(iii) Octagon
(iv) x-axis or y-axis.
(b)
Question 6:
(a) If a, b, c are in continued proportion, prove that (a + b + c) (a – b + c) = a2 + b2 + c2. [3]
(b) In the given figure ABC is a triangle and BC is parallel to the y-axis. AB and AC intersects the y-axis at P and Q respectively.
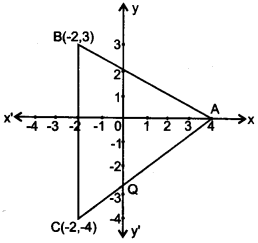
(i) Write the coordinates of A.
(ii) Find the length of AB and AC.
(iii) Find the ratio in which Q divides AC.
(iv) Find the equation of the line AC. [4]
(c) Calculate the mean of the following distribution :
| Class Interval | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Frequency | 8 | 5 | 12 | 35 | 24 | 16 |
Solution:
(a)
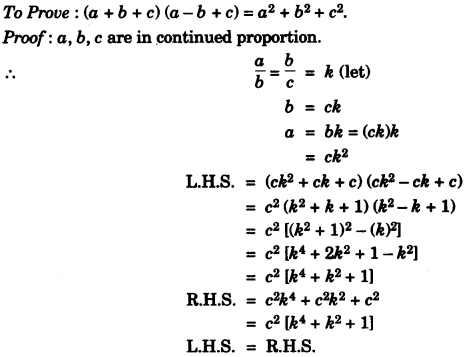
(b) (i) Coordinates of A (4,0)
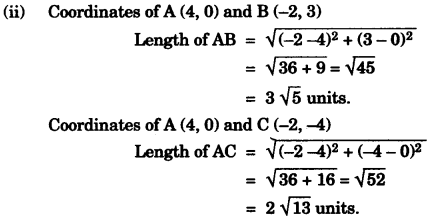
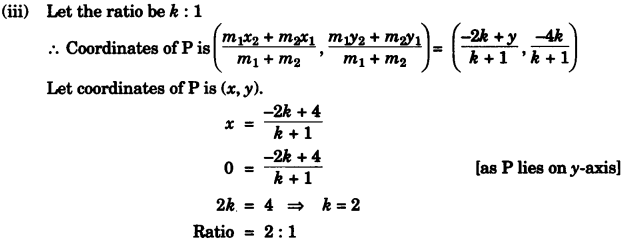
(iv) Equation of AC
Coordinates of A(4, 0) and C(-2, -4)
y−0=0+44+2(x−4)
3y = 2x – 8
2x – 3y – 8 = 0
(c)
| Class | Mid value (x) | f | fx |
| 0-10 | 5 | 8 | 40 |
| 10-20 | 15 | 5 | 75 |
| 20-30 | 25 | 12 | 300 |
| 30-40 | 35 | 35 | 1225 |
| 40-50 | 45 | 24 | 1080 |
| 50-60 | 55 | 16 | 880 |
| Total | 100 | 3600 |
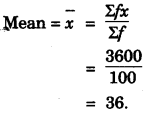
Question 7:
(a) Two solid spheres of radii 2 cm and 4 cm are melted and recast into a cone of height 8 cm. Find the radius of the cone so formed. [3]
(b) Find ‘a’ if the two polynomials ax3 + 3x2 – 9 and 2x3 + 4x + a, leaves the same remainder when divided by x + 3. [3]
![]()
Solution:
(a)
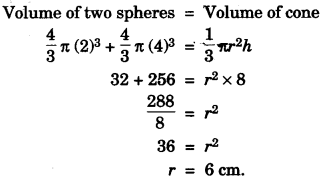
(b)

(c)

Question 8:
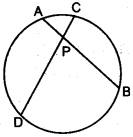
(a) AB and CD are two chords of a circle intersecting at P. Prove that AP × PB = CP × PD. [3]
(b) A bag contains 5 white balls, 6 red balls and 9 green balls. A ball is drawn at random from the bag. Find the probability that the ball drawn is:
(i) a green ball.
(ii) a white or a red ball
(iii) is neither a green ball nor a white ball. [3]
(c) Rohit invested Rs. 9,600 o Rs. 100 shares at Rs. 20 premium paying 8% dividend,. Rohit sold the shares when the price rose to 1 160. He invested the proceeds (excluding dividend) in 10% Rs. 50 shares at Rs. 40. Find the:
(i) original number of shares.
(ii) sale proceeds.
(iii) new number of shares.
(iv) change in the two dividends.
Solution:
(a)

(b) White – 5 , Red – 6 , Green – 9

(c)

Question 9:
(a) The horizontal distance between two towers is 120m. The angle of elevation of the top and angle of depression of the bottom of the first tower as observed from the second tower is 30° and 24° respectively.
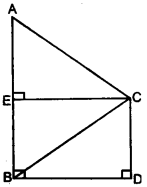
Find the height of the two towers. Give your answer correct to 3 significant figures. [4]
(b) The weight of 50 workers is given below:
| Weight in Kg | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 |
| No. Workers | 4 | 7 | 11 | 14 | 6 | 5 | 3 |
Draw an ogive of the given distribution using a graph sheet. Take 2 cm = 10 kg on one axis and 2 cm = 5 workers along the other axis. Use a graph to estimate the following:
(i) the upper and lower quartiles.
(ii) if weighing 95 kg and above is considered overweight find the number of workers who are overweight. [6]
Solution:
(a)
(b)
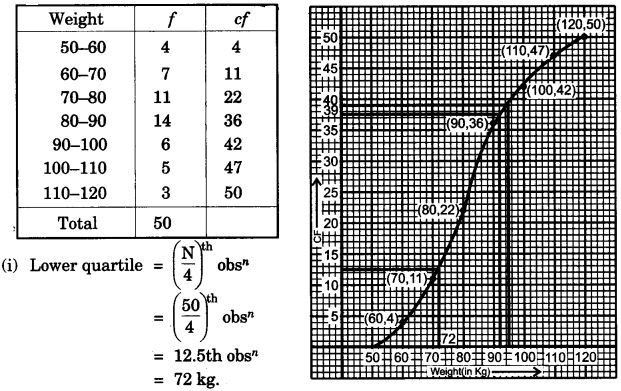

Question 10:
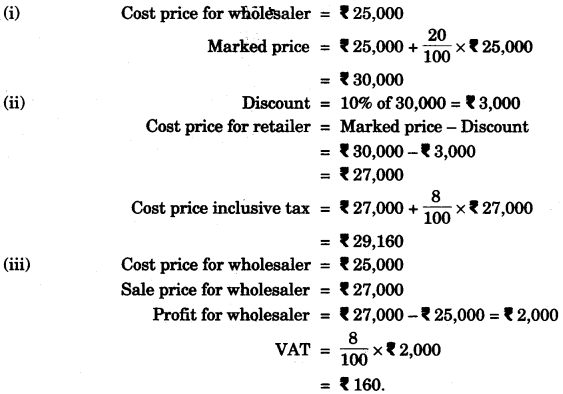
(a) A wholesaler buys a TV from the manufacturer for Rs. 25,000. He marks the price of the TV 20% above his cost price and sell it to a retailer at 10% discount on the marked price. If the rate of VAT is 8%, find the:
(i) marked price.
(ii) retailer’s cost price inclusive of tax.
(iii) VAT paid by the wholesaler. [3]
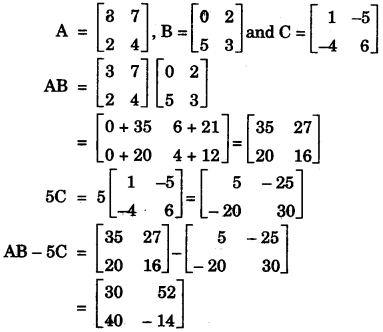
(b) If A = [3724], B = [0253], C = [1−5−46]. Find AB – 5C. [3]
(c) ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC.
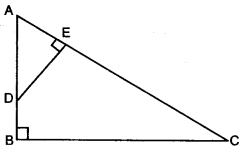
Prove that:
(i) ∆ADE ~ ∆ACB.
(ii) If AC = 13 cm, BC = 5 cm and AE – 4 cm. Find DE and AD.
(iii) Find, area of ∆ ADE: area of quadrilateral BCED. [4]
Solution:
(a)
(b)
(c)

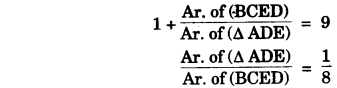
Question 11:
(a) Sum of two natural numbers is 8 and the difference of their reciprocal is 215. Find the numbers. [3]
![]()
(c) Construct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°. Hence
(i) Construct the locus of points equidistant from BA and BC.
(ii) Construct the locus of points equidistant from B and C.
(iii) Mark the point which satisfies the above two loci as P. Measure and write the length of PC. [4]
Solution:
(a)
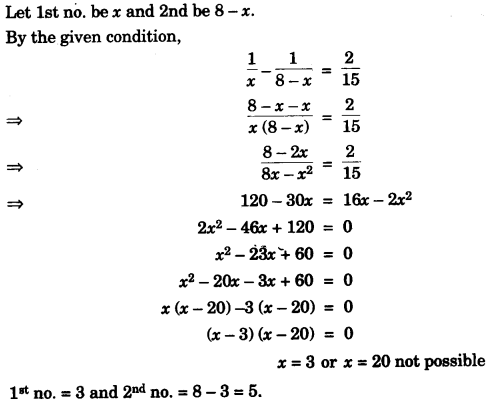
(b)
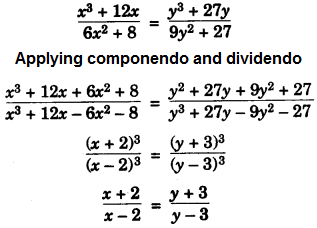
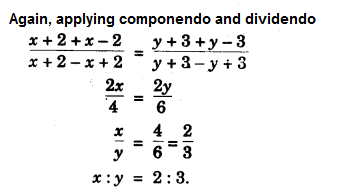
(c) Steps of Construction:
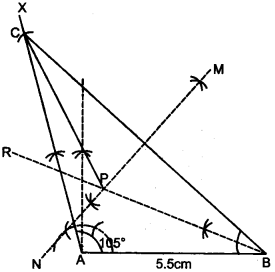
(i) Draw a line AB = 5.5 cm.
(ii) With the help of the point A, draw ∠XAB = 105°.
(iii) Taking radius 6 cm, cut AC = 6 cm and join C to B.
(iv) Draw perpendicular bisector of BC and angle of bisector ∠CBA; both intersecting at P.
P is the required point.
PC = 4.8 cm.
