ICSE Maths Previous Year Question Paper 2013 Solved for Class 10
ICSE Paper 2013
MATHEMATICS
(Two hours and a half)
Answers to this Paper must be written on the paper provided separately.
You will not be allowed to write during the first 15 minutes.
This time is to be spent in reading the question paper.
The time given at the head of this Paper is the time allowed for writing the answers.
Attempt all questions from Section A and any four questions from Section B.
All working, including rough work, must be clearly shown and must be done on the same sheet as the rest of the answer. Omission of essential working will result in the loss of marks.
The intended marks for questions or parts of questions are given in brackets [ ].
Mathematical tables are provided.
SECTION-A (40 Marks)
(Attempt all questions from this Section)
Question 1:
(a)
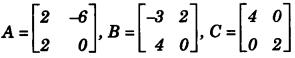
Find the matrix X such that A + 2X = 2B + C. [3]
(b) At what rate % p.a. will a sum of Rs. 4000 yield Rs. 1324 as compound interest in 3 years? [3]
(c) The median of the following observations 11, 12, 14, (x – 2), (x + 4), (x + 9), 32, 38, 41 arranged in ascending order is 24. Find the value of x and hence find the mean. [4]
Solution:
(a)
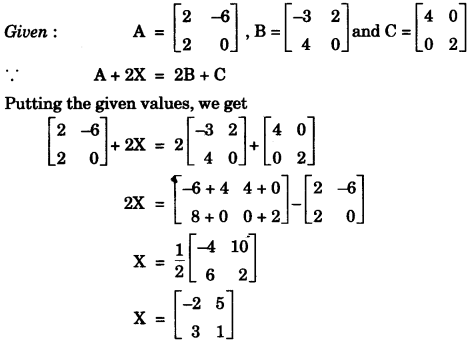
(b)
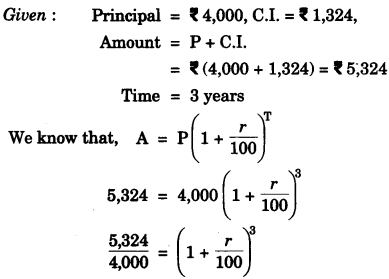

(c)

Question 2:
(a) What number must be added to each of the number 6, 15, 20 and 43 to make them proportional? [3]
(b) If (x – 2) is a factor of the expression 2x3 + ax2 + bx – 14 and when the expression is divided by (x – 3), it leaves a remainder 52, find the values of a and b. [3]
(c) Draw a histogram from the following frequency distribution and find the mode from the graph: [4]
| Class | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 |
| Frequency | 2 | 5 | 18 | 14 | 8 | 5 |
Solution:
(a)

(b)

(c)
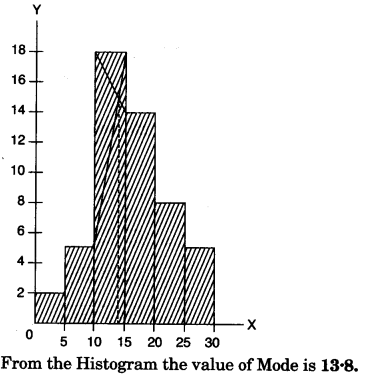
Question 3:

(c) AB is a diameter of a circle with centre C = (-2, 5). If A = (3, -7). Find:
(i) The length of radius AC
(ii) The coordinates of B.
Solution:


(c)

Question 4:
(a) Solve the following equation and calculate the answer correct to two decimal places:
(c) Using graph paper, plot the points A(6, 4) and B(0, 4).
(i) Reflect A and B in the origin to get the images A’ and B’.
(ii) Write the co-ordinates of A’ and B’.
(iii) State the geometrical name for the figure ABA’B’.
(iv) Find its perimeter. [4]
Solution:
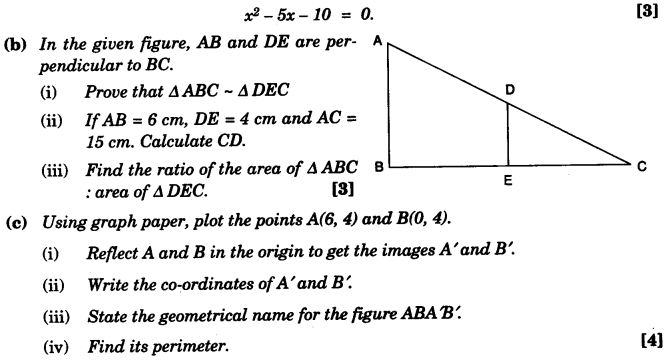
(a) Given: x2 – 5a – 10 = 0
Here, a = 1, b = – 5 and c = – 10
(b)
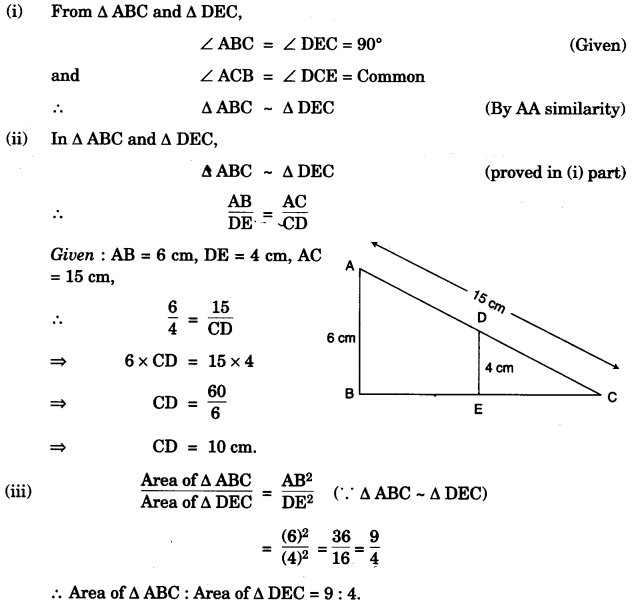
(c)
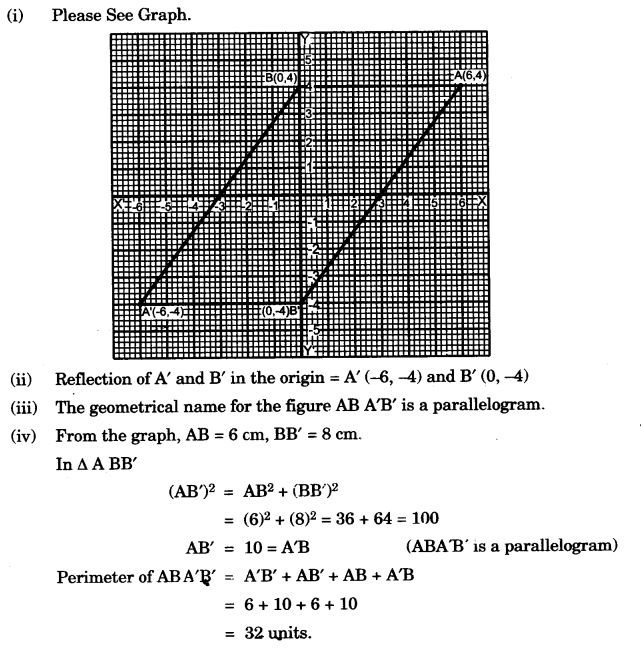
SECTION-B (40 Marks)
(Attempt any four questions from this Section)
Question 5:
(a) Solve the following inequation, write the solution set and represent it on the number line: [3]
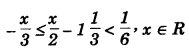
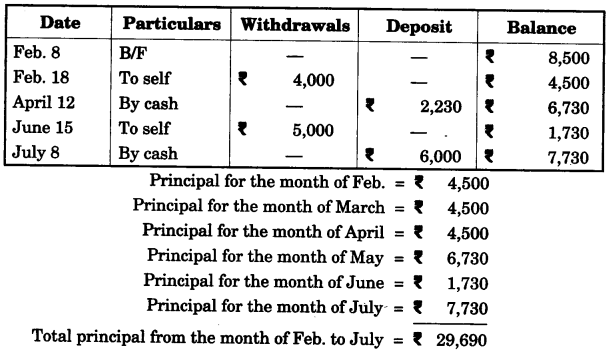
(b) Mr. Britto deposits a certain sum of money each month in a Recurring Deposit Account of a bank. If the rate of interest is of 8% per annum and Mr. Britto gets Rs. 8088 from the bank after 3 years, find the value of his monthly installment. [3]
(c) Salman buys 50 shares of face value Rs. 100 available at Rs. 132.
(i) What is his investment?
(ii) If the dividend is 7.5%, what will be his annual income?
(iii) If he wants to increase his annual income by Rs. 150, how many extra shares should he buy? [4]
Solution:
(a)
(b)

(c)
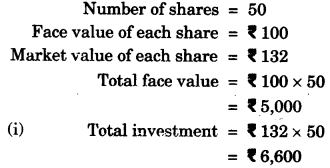
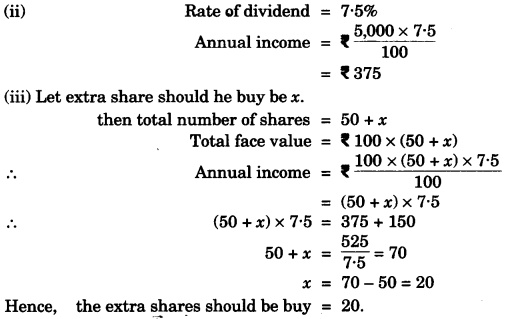
Question 6:
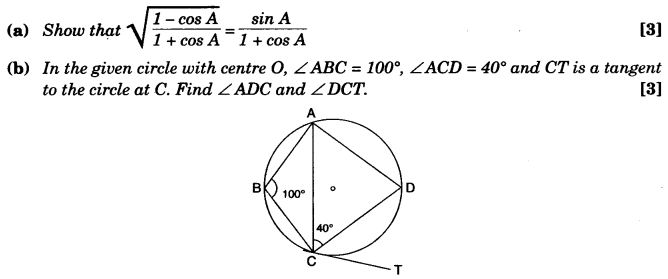

Solution:
(a)
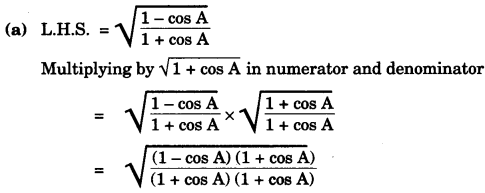
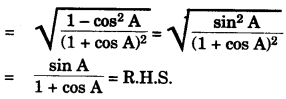
(b)
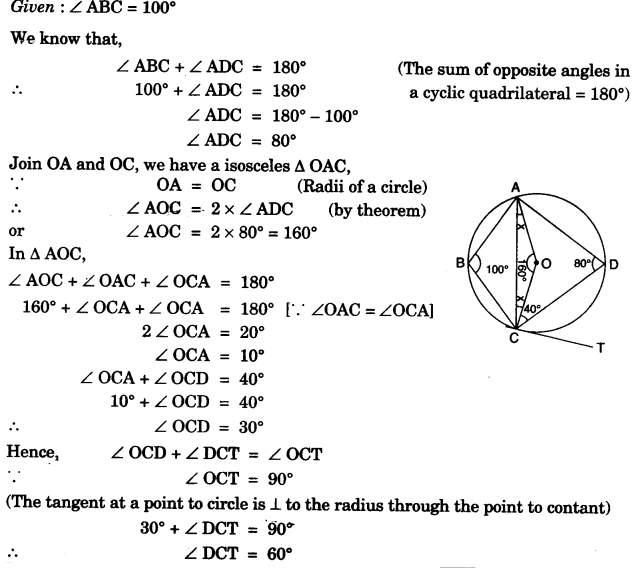
(c)
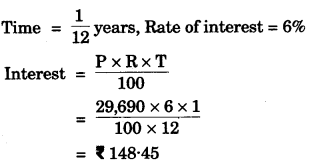
Question 7:
(a) In ΔABC, A(3, 5), B(7, 8) and C(1, -10). Find the equation of the median through A. [3]
(b) A shopkeeper sells an article at the listed price of Rs. 1,500 and the rate of VAT is 12% at each stage of sale. If the shopkeeper pays a VAT of Rs. 36 to the Government, what was the price, inclusive of Tax, at which the shopkeeper purchased the article from the wholesaler? [3]
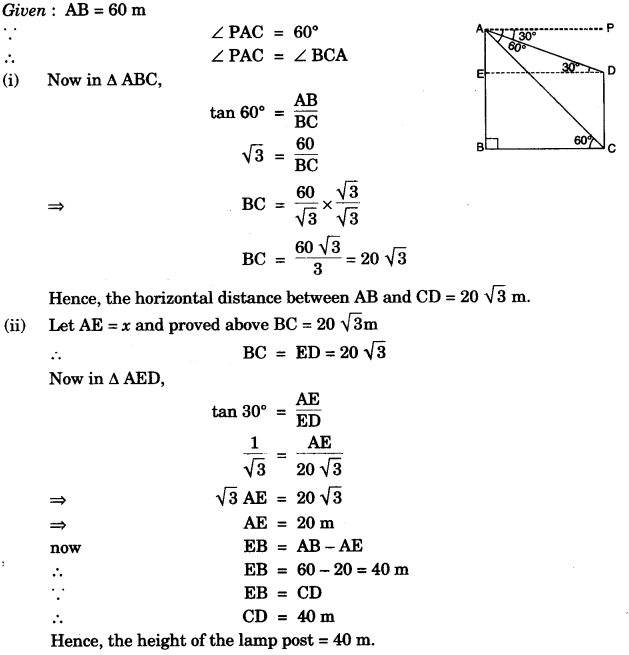
(c) In the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30° and 60° respectively. Find:
(i) The horizontal distance between AB and CD.
(ii) The height of the lamp post.
Solution:
(a)


(c)
Question 8:
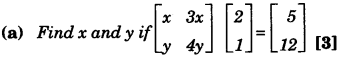
(b) A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast. [3]
(c) Without solving the following quadratic equation, find the value of ‘p’ for which the given equation has real and equal roots: x2 + (p – 3)x + p = 0 [4]
Solution:
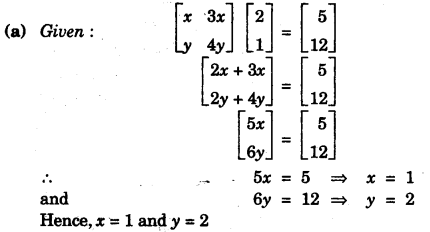
(b)

(c)
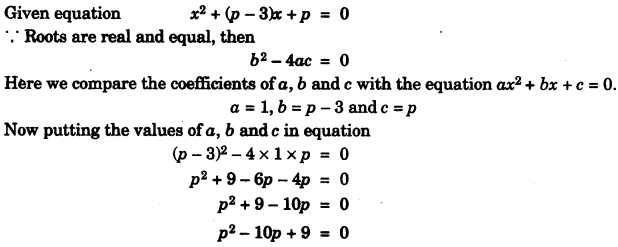
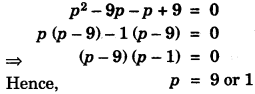
Question 9:
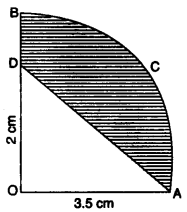
(a) In the figure alongside, OAB is a quadrant of a circle. The radius OA = 3.5 cm and OD = 2 cm. Calculate the area of the shaded portion. (Take π = 22/7) [3]
(b) A box contains some black balls and 30 white balls. If the probability of drawing a black ball is two-fifths of a white ball, find the number of black balls in the box. [3]
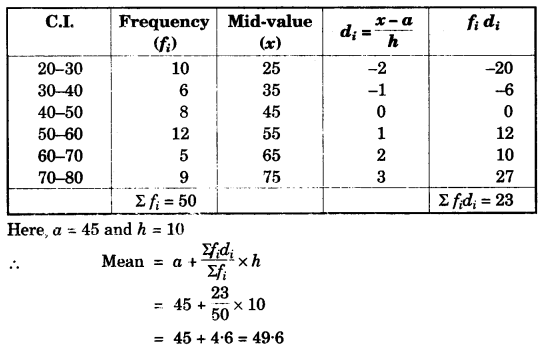
(c) Find the mean of the following distribution by step deviation method:
| Class Interval | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Frequency | 10 | 6 | 8 | 12 | 5 | 9 |
Solution:
(a)

(b)

(c)
Question 10:
(a) Using a ruler and compasses only:
(i) Construct a triangle ABC with the following data:
AB = 3.5 cm, BC = 6 cm and ∠ABC = 120°
(ii) In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
(iii) Measure ∠BCP. [3]
(b) The mark obtained by 120 students in a test are given below:
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No of Students | 5 | 9 | 16 | 22 | 26 | 18 | 11 | 6 | 4 | 3 |
Draw an ogive for the given distribution on a graph sheet.
Using suitable scale for ogive to estimate the following:
(i) The median
(ii) The number of students who obtained more than 75% marks in the test.
(iii) The number of students who did not pass the test if minimum marks required to pass is 40. [6]
Solution:
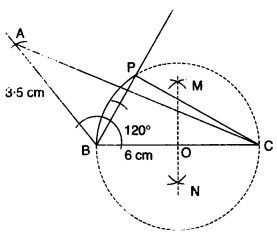
(a) Steps of Construction:
(i) Draw a line BC = 6 cm.
(ii) With the help of the point B, draw ∠ABC = 120°.
(iii) Taking radius 3.5 cm cut BA = 3.5 cm.
(iv) Join A to C.
(v) Draw ⊥ bisector MN of BC.
(vi) Draw a circle 0 as centre and OC as radius.
(vii) Draw angle bisector of ∠ABC which intersects circle at P.
(viii) Join BP and CP.
(ix) Now, ∠BCP = 30°.
(b)
| Marks | No. of Students (f) | Cumulative Frequency |
| 0-10 | 5 | 5 |
| 10-20 | 9 | 14 |
| 20-30 | 16 | 30 |
| 30-40 | 22 | 52 |
| 40-50 | 26 | 78 |
| 50-60 | 18 | 96 |
| 60-70 | 11 | 107 |
| 70-80 | 6 | 113 |
| 80-90 | 4 | 117 |
| 90-100 | 3 | 120 |
| n = 120 |
On the graph paper, we plot the following points:
(10, 5), (20, 14), (30, 30), (40, 52), (50, 78), (60, 96). (70, 107), (80, 113), (90, 117), (100, 120).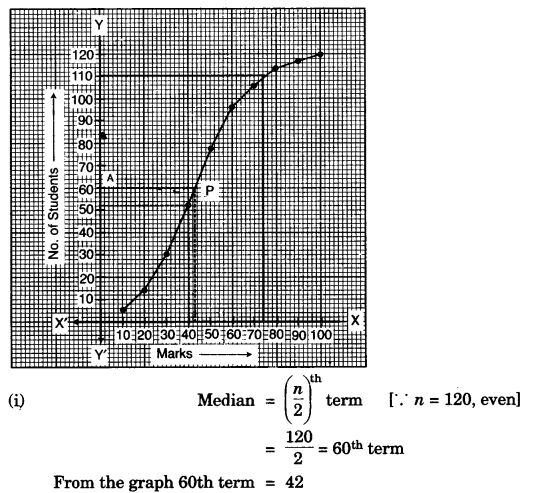
(ii) The number of students who obtained more than 75% marks in test
= 120 – 110 = 10.
(iii) The number of students who did not pass the test if the minimum pass marks 40 = 52.
Question 11:
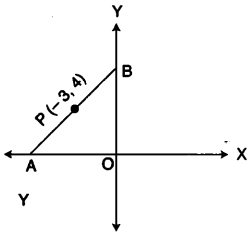
(a) In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P(-3, 4) on AB divides it in the ratio 2:3. Find the coordinates of A and B. [3]
(b) Using the properties of proportion, solve for x, given [3]
![]()
(c) A shopkeeper purchases a certain number of books for Rs. 960. If the cost per book was 18 less, the number of books that could be purchased for Rs. 960 would be 4 more. Write an equation, taking the original cost of each book to be Rs. x, and solve it to find the original cost of the books. [4]
Solution:
(a)

(b)
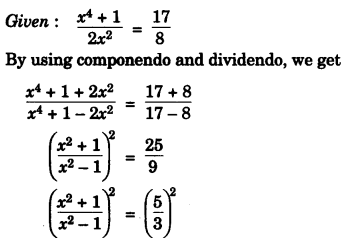

(c)

