Horizontal Shift – Phase Shift
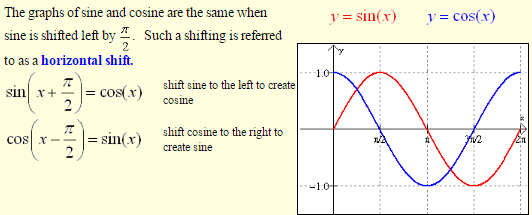
horizontal shift and phase shift:
If the horizontal shift is positive, the shifting moves to the right. If the horizontal shift is negative, the shifting moves to the left.
From the sinusoidal equation,
y = A sin (B(x-C)) + D
the horizontal shift is obtained by determining the change being made to the x value.
The horizontal shift is C.
When the value B = 1, the horizontal shift, C, can also be called a phase shift, as seen in the diagram at the right.
The easiest way to determine horizontal shift is to determine by how many units the “starting point” (0,0) of a standard sine curve, y = sin(x), has moved to the right or left.
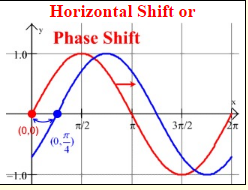

They make a distinction between y = Asin(B(x – C)) + D and y = Asin(Bx – C) + D,
calling the phase shift C in the first equation when B = 1, otherwise calling it C in the second equation.
While this distinction exists for physicists and engineers, some mathematics textbooks use the terms “horizontal shift” and “phase shift” to mean the same thing. Refer to your textbook, or your instructor, to see what definition they wish you to use for “phase shift”, if they are using that term. We will be discussing “horizontal shifts”.
Horizontal shifts can be applied to all trigonometric functions.
