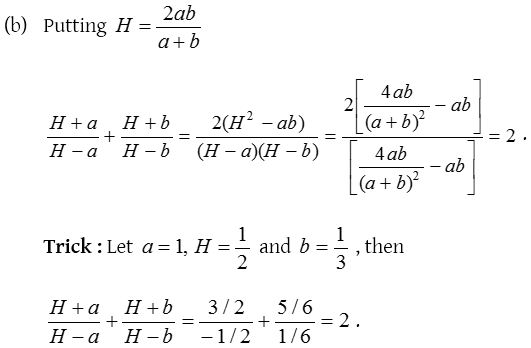What is Harmonic Progression in Mathematics?

What is Harmonic Progression in Mathematics?

Harmonic Progression (H.P.)

Definition:
A progression is called a harmonic progression (H.P.) if the reciprocals of its terms are in A.P.

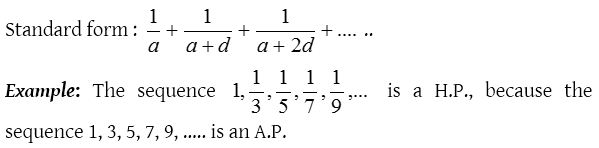
General term of an H.P.

Harmonic mean

If three or more numbers are in H.P., then the numbers lying between the first and last are called harmonic means (H.M.’s) between them. For example 1, 1/3, 1/5, 1/7, 1/9 are in H.P. So 1/3, 1/5 and 1/7 are three H.M.’s between 1 and 1/9.
Also, if a, H, b are in H.P., then H is called harmonic mean between a and b.
(1) Insertion of harmonic means
(i) Single H.M. between a and b \(=\frac { 2ab }{ a+b }\).
(ii) H, H.M. of n non-zero numbers a₁, a₂, a₃, ….. a_n is given by

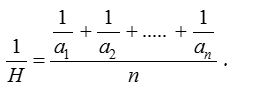
(iii) Let a, b be two given numbers. If n numbers H₁, H₂, H₃, ….. H_n are inserted between a and b such that the sequence  a, H₁, H₂, H₃, ….. H_n, b is a H.P., then H₁, H₂, H₃, ….. H_n are called n harmonic means between a and b.

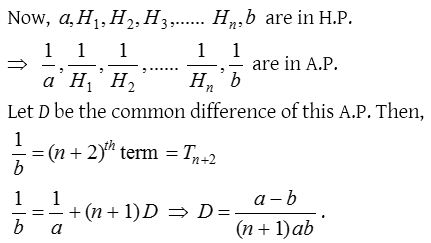
Thus, if n harmonic means are inserted between two given numbers a and b, then the common difference of the corresponding A.P. is given by

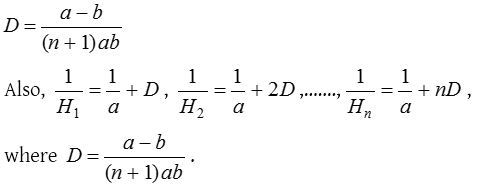
Properties of H.P.

1. No term of H.P. can be zero.
2. If H is the H.M. between a and b, then
   

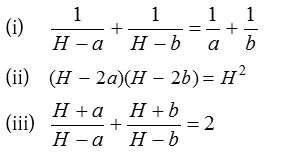
Harmonic Progression Problems with Solutions

1.

Solution:

2.

Solution:

3.

Solution:

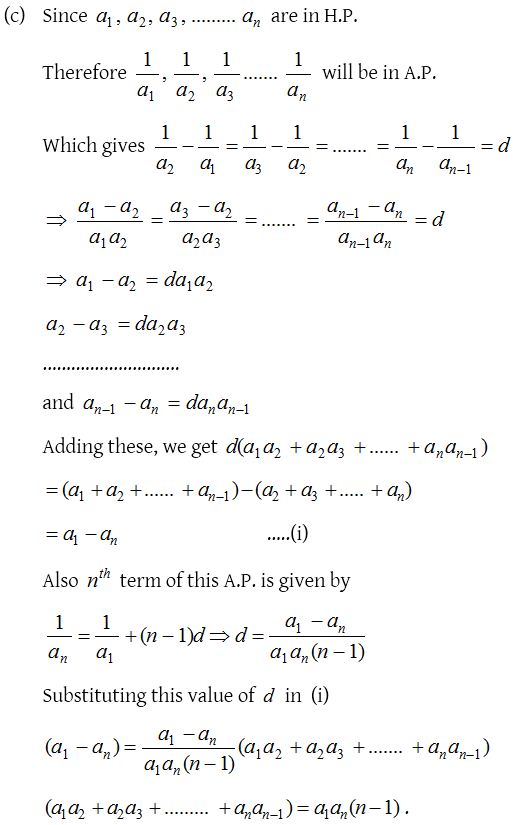
4.

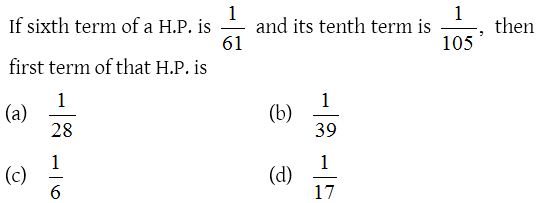
Solution:

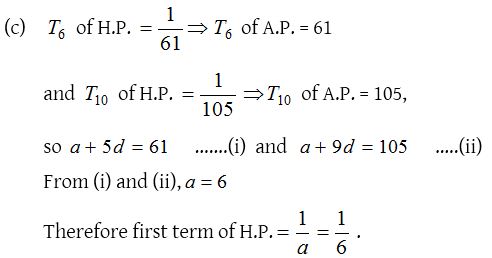
5.

Solution:

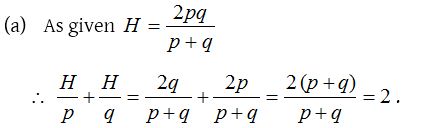
6.

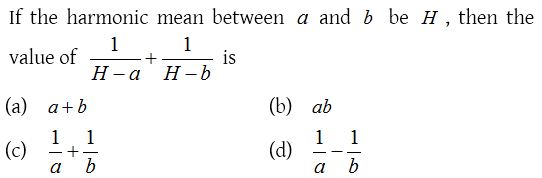
Solution:

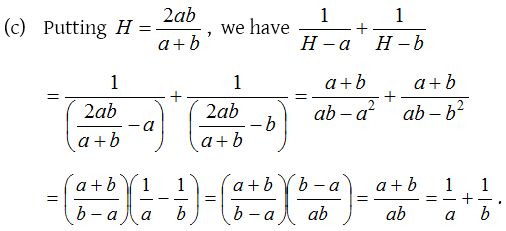
7.

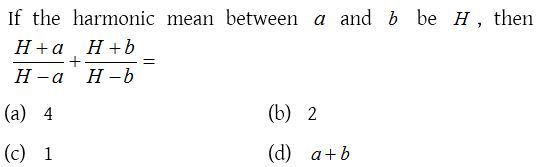
Solution: