Graphing, Domain and Range of Functions
The domain is the set of all first elements of ordered pairs (x-coordinates).
The range is the set of all second elements of ordered pairs (y-coordinates).
Domain and range can be seen clearly from a graph.
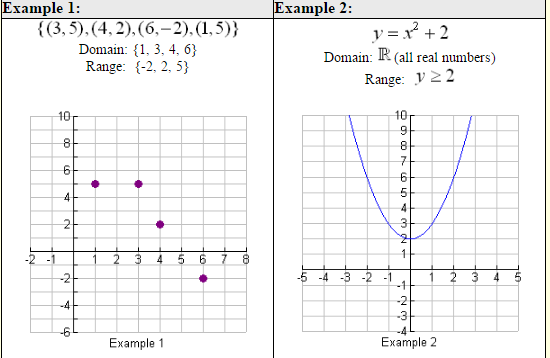
The two examples shown above are functions. But, as we know, not all graphs are functions.
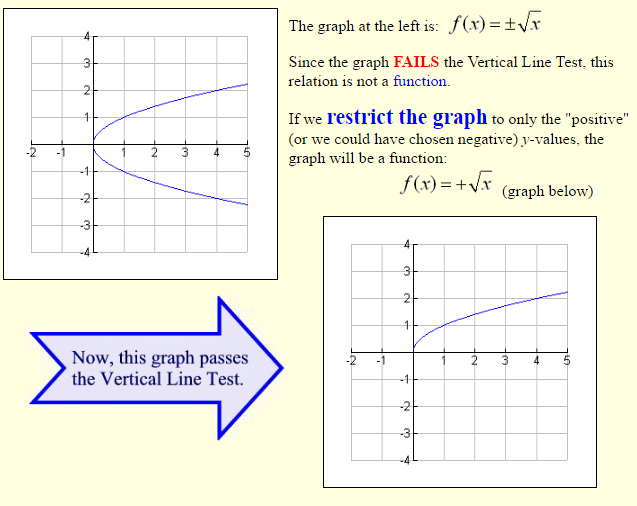
In a similar fashion, we can also restrict domains to ensure that graphs are functions.
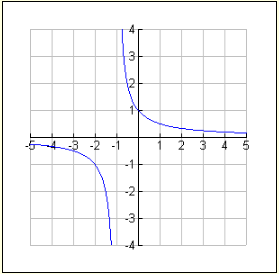
The graph at the left is: f(x) = 1/x+1
If the domain for this graph is listed as “all Real numbers”, this relation is NOT a function. At first glance this graph appears to pass the Vertical Line Test, but it is actually undefined at x = -1.
If we restrict the domain to be “all Real numbers excluding -1”, our relation will be a function.
Domain: R-[-1]
