Gradient (Slope) of a Straight Line
The straight line is a curve such that every point on the line segment joining any two points on it lies on it. The simplest locus of a point in a plane is a straight line.
 A line is determined uniquely by any one of the following:
A line is determined uniquely by any one of the following:
- Two different points (because we know the axiom that one and only one straight line passes through two given points).
- A point and a given direction.
Slope (Gradient) of a line
The trigonometrical tangent of the angle that a line makes with the positive direction of the x-axis in anticlockwise sense is called the slope or gradient of the line.
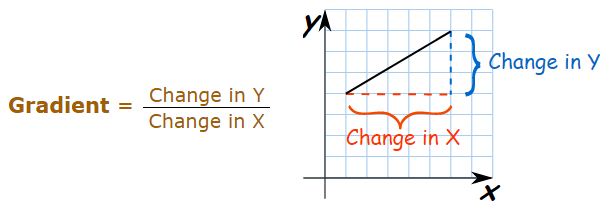 The slope of a line is generally denoted by m. Thus, m = tan θ.
The slope of a line is generally denoted by m. Thus, m = tan θ.
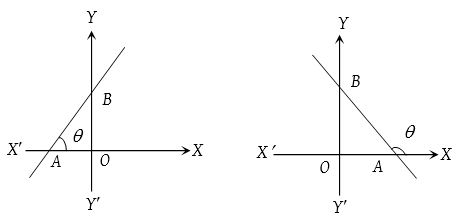
- Slope of line parallel to x – axis is m = tan 0° = 0.
- Slope of line parallel to y – axis is m = tan 90° = ∞.
- Slope of the line equally inclined with the axes is 1 or – 1.
- Slope of the line through the points A(x1, y1) and B(x2, y2) is y2−y1x2−x1 taken in the same order.
- Slope of the line ax + by + c = 0, b ≠ 0 is −ab.
- Slope of two parallel lines are equal.
- If m1 and m2 be the slopes of two perpendicular lines, then m1.m2 = −1.
- m can be defined as tan θ for 0 ≤ θ ≤ π and θ ≠ π/2.
