What is a Geometric Progression?
Geometric Progression (G.P.)
Definition:
A progression is called a G.P. if the ratio of its each term to its previous term is always constant. This constant ratio is called its common ratio and it is generally denoted by r.

Example:
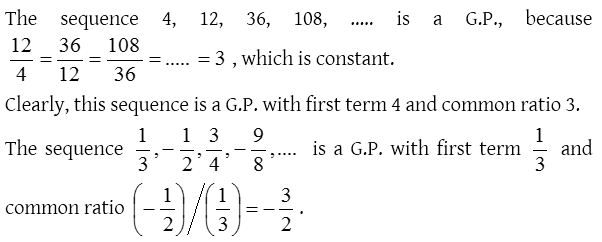
General term of a G.P.
(1) We know that a, ar, ar2, ar3, ……. arn−1 is a sequence of G.P.
Here, the first term is ‘a’ and the common ratio is ‘r’.
The general term or nth term of a G.P. is Tn = arn−1.
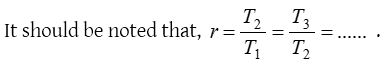
(2) pth term from the end of a finite G.P. : If G.P. consists of ‘n’ terms, pth term from the end = (n – p + 1)th term from the beginning = arn–p.
Also, the pth term from the end of a G.P. with last term l and common ratio r is
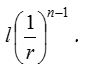
Selection of terms in a G.P.
(1) When the product is given, the following way is adopted in selecting certain number of terms :
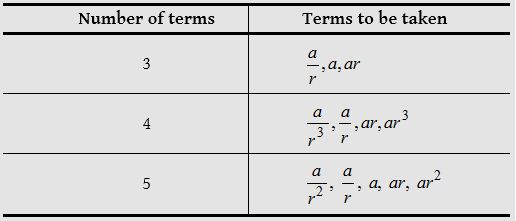
(2) When the product is not given, then the following way is adopted in selection of terms
| Number of terms | Terms to be taken |
| 3 | a, ar, ar2 |
| 4 | a, ar, ar2, ar3 |
| 5 | a, ar, ar2, ar3, ar4 |
Sum of first ‘n’ terms of a G.P.
If a be the first term, r the common ratio, then sum of first n terms of a G.P. is given by
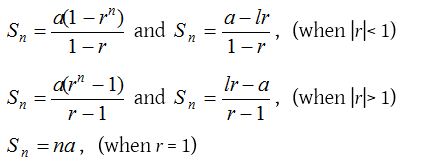
Sum of infinite terms of a G.P.
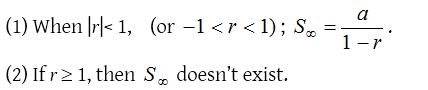
Geometric mean
Properties of G.P.
- If all the terms of a G.P. be multiplied or divided by the same non-zero constant, then it remains a G.P., with the same common ratio.
- The reciprocal of the terms of a given G.P. form a G.P. with common ratio as reciprocal of the common ratio of the original G.P.
- If each term of a G.P. with common ratio r be raised to the same power k, the resulting sequence also forms a G.P. with common ratio rk.
- In a finite G.P., the product of terms equidistant from the beginning and the end is always the same and is equal to the product of the first and last term. i.e., if a1, a2, a3, …… an be in G.P.
Then a1an = a2an-1 = a3an-2 = a4an-3 = ar.an-r+1 - If the terms of a given G.P. are chosen at regular intervals, then the new sequence so formed also forms a G.P.
- If a1, a2, a3, …… an is a G.P. of non-zero, non-negative terms, then log a1, log a2, log a3, …… log an is an A.P. and vice-versa.
- Three non-zero numbers a, b, c are in G.P., iff b2 = ac.
- If first term of a G.P. of n terms is a and last term is l, then the product of all terms of the G.P. is (al)n/2.
- If there be n quantities in G.P. whose common ratio is r and Sm denotes the sum of the first m terms, then the sum of their product taken two by two is rr+1SnSn−1.
- If ax1, ax2, ax3, ……, axn are in G.P., then x1, x2, x3 …… xn will be are in A.P.
Geometric Progression Problems with Solutions
1. If the and terms of a G.P. be respectively, then the relation between is

Solution:
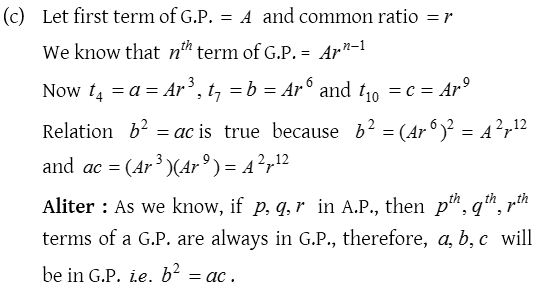
2.
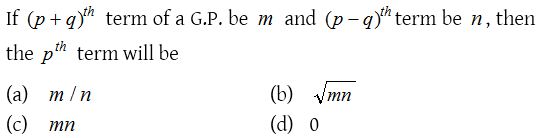
Solution:

3.
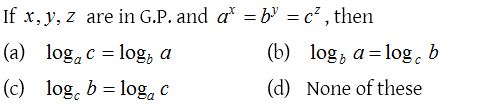
Solution:
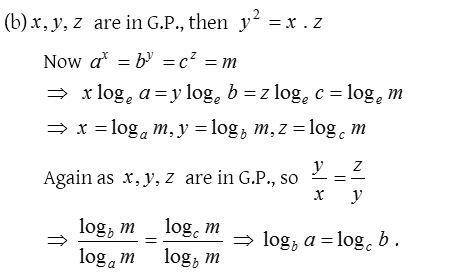
4.
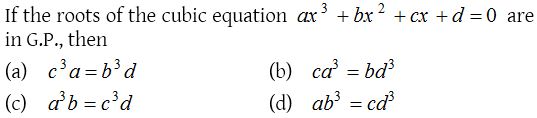
Solution:
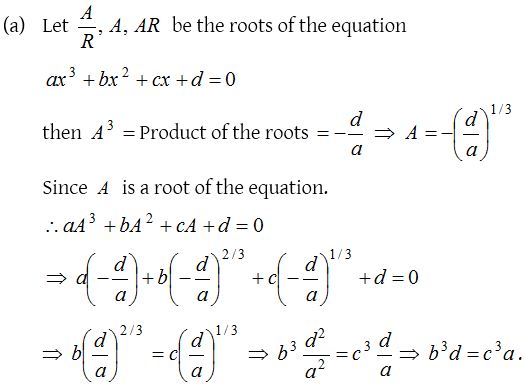
5.
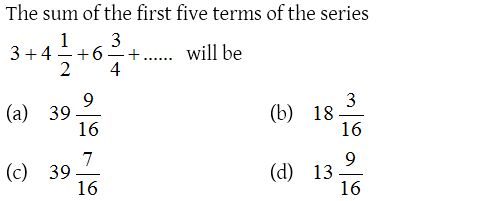
Solution:
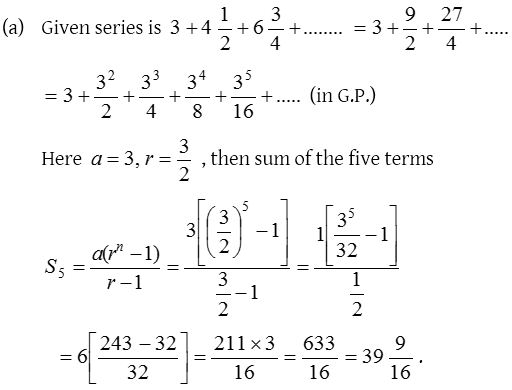
6.
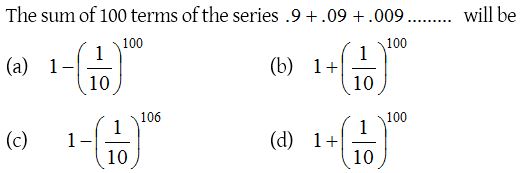
Solution:
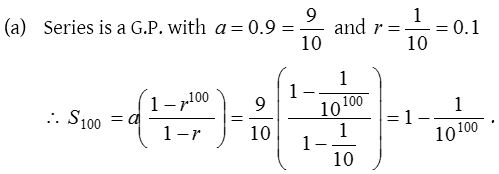
7.
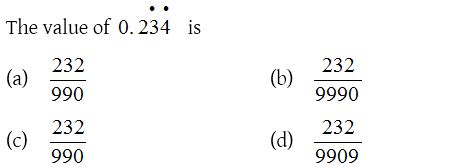
Solution:

8.
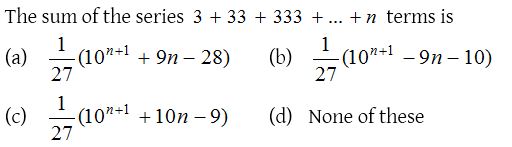
Solution:

