How do you know if a Function is Increasing or Decreasing?
Increasing and decreasing functions
Definition:
(1) A function f is said to be an increasing function in ]a,b[, if x1 < x2 ⇒ f(x1) < f(x2) for all x1, x2 ∈ ]a,b[.
(2) A function f is said to be a decreasing function in ]a,b[, if x1 < x2 ⇒ f(x1) < f(x2), ∀ x1, x2 ∈ ]a,b[.
f(x) is known as non-decreasing if f’(x) ≥ 0 and non-increasing if f’(x) ≤ 0.
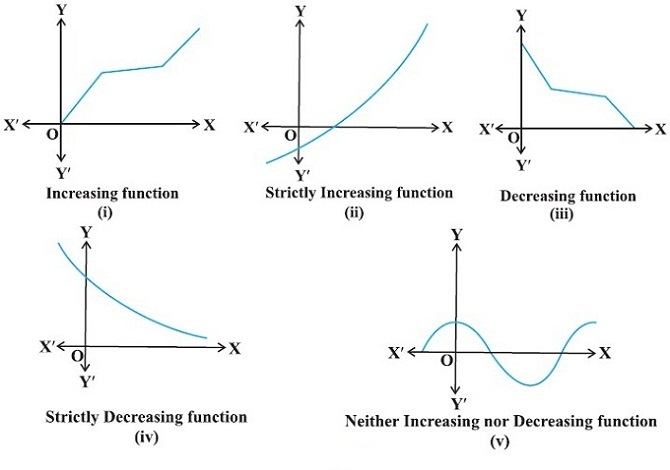
Monotonic function: A function f is said to be monotonic in an interval if it is either increasing or decreasing in that interval.
We summarize the results in the table below :
| f’(a1) | f’’(a1) | f’’’(a1) | Behaviour of f at a1 |
| + | Increasing | ||
| – | Decreasing | ||
| 0 | + | Minimum | |
| 0 | – | Maximum | |
| 0 | 0 | ? | |
| 0 | 0 | ± | Inflection |
| 0 | 0 | ? |
- Blank space indicates that the function may have any value at a1.
- Question mark indicates that the behaviour of f cannot be inferred from the data.
Properties of monotonic functions
- If f(x) is a strictly increasing function on an interval [a, b], then f−1 exists and it is also a strictly increasing function.
- If f(x) is a strictly increasing function on an interval [a, b] such that it is continuous, then f−1 is continuous on [f(a), f(b)].
- If f(x) is continuous on [a, b] such that f’(c) ≥ 0 [f’(c) > 0] for each c ∈ (a, b), then f(x) is monotonically (strictly) increasing function on [a, b].
- If f(x) is continuous on such that f’(c) ≤ 0 [f’(c) > 0] for each c ∈ (a, b), then f(x) is monotonically (strictly) decreasing function on [a, b].
- If f(x) and g(x) are monotonically (or strictly) increasing (or decreasing) functions on [a, b], then is a monotonically (or strictly) increasing function on [a, b].
- If one of the two functions f(x), g(x) is strictly (or monotonically) increasing and other a strictly (monotonically) decreasing, then gof(x) is strictly (monotonically) decreasing on [a, b].
