Frank ICSE Solutions for Class 9 Maths Mid-point and Intercept Theorems Ex 15.2
Ex No: 15.2
Solution 1:
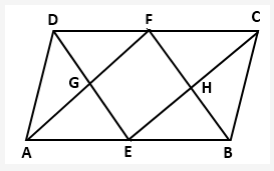

Solution 2:
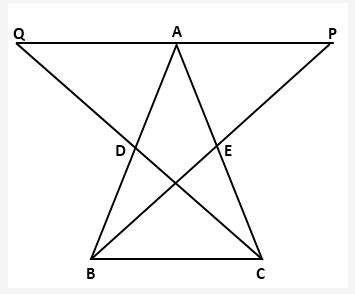

Solution 3:
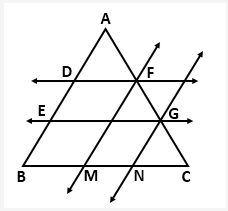

Solution 4:

Solution 5:
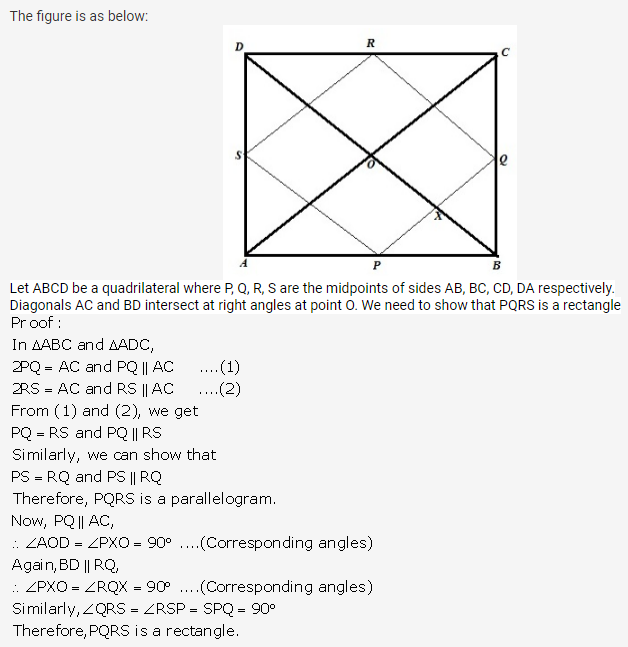
Solution 6:
Note: This question is incomplete.
According to the information given in the question,
F could be any point on BC as shown below:
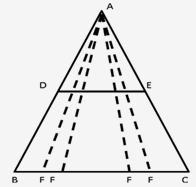
So, this makes it impossible to prove that DP = DE, since P too would shift as F shift because P too would be any point on DE as F is.
Note: If we are given F to be the mid-point of BC, the result can be proved.

Solution 7:
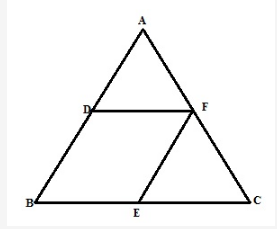
From the figure EF ∥ AB and E is the midpoint of BC.
Therefore, F is the midpoint of AC.
Here EF ∥ BD, EF = BD as D is the midpoint of AB.
BE ∥ DF, BE = DF as E is the midpoint of BC.
Therefore BEFD is a parallelogram.
Remark: Figure modified
Solution 8:

Solution 9:

