How do you figure out Rotational Symmetry?
Rotational Symmetry
If a shape can fit exactly into itself after a certain rotation (not a full one) about a fixed point (called centre of rotation) then it is said to have rotational symmetry.
The angle of turning during rotation is called the angle of rotation.
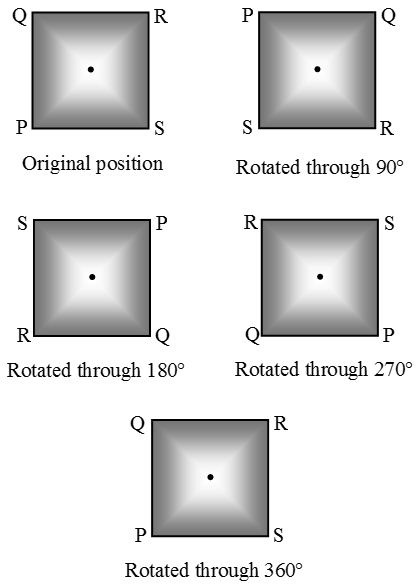
For example, a square has a rotational symmetry.
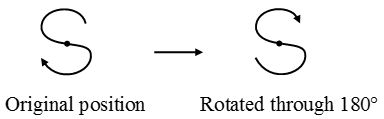
Point Symmetry
Some figures appear to be in the same position when rotated through half turn (180°) about a fixed point, they are said to have point symmetry.
 Note:
Note:
- A square has line symmetry as well as rotational symmetry.
- An equilateral triangle has rotational symmetry as well as line symmetry
- A full rotation does not mean that a figure has rotational symmetry as every shape could fit exactly into itself after a full rotation.
Order of Rotational Symmetry
The number of times a shape fits onto itself in one complete turn is called the order of rotational symmetry.
or
Thus, we say that the order of the rotational symmetry of a figure with a point marked (say P), is the number of rotations about a fixed point required to bring back the marked point P to its original position.
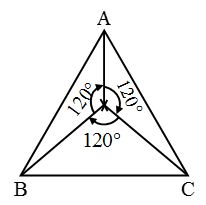
For example, an equilateral triangle has rotational symmetry of order 3 as there are three positions where it appears not to have moved.
Note:
The figures which do not have rotational symmetry are said to have rotational symmetry of order 1.
Direction of Rotation
The body moving in the direction of hands of clock is said to have clockwise rotation and if it moves in reverse direction of hands of clock is said to have anticlock rotation.
Thus, we can find the order of rotation of a figure by dividing 360° by the measure of the angle rotated by the original figure when it looks just the same as before.
For example, for an equilateral triangle ABC, when it is rotated about point X, will take the same shape after a rotation of angle 120° as in figure.
Thus, order of rotational symmetry = 360°/120° = 3.
Note that we found the same order when we rotated figure
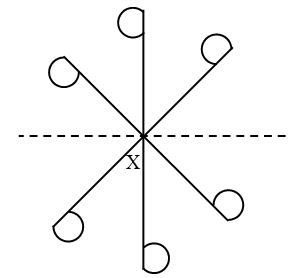
 Example: Find the order of rotational symmetry about point X of the following figure:
Example: Find the order of rotational symmetry about point X of the following figure:
 Solution:
Solution:
Draw a dotted line passing through the point X.
Make a copy of the figure on a tracing paper.
Put the traced copy on the figure and pin up by a thumb-tack at point X.
Rotate the figure (clockwise or anticlockwise). Stop when the traced copy completely overlaps the original figure first time during rotation.
Now put a protractor with its zero at X and measure the angle formed by the dotted lines (one line on the figure and other on the traced copy).
We find that the measure of the angle thus formed is 60° as shown in figure.
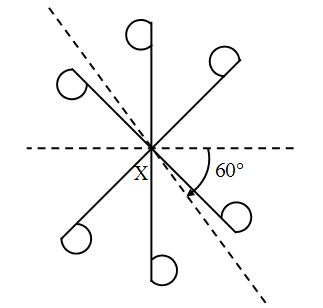 Similarly, again rotate about X and measure the angle formed between the two dotted lines, when the original figure and the traced copy again look just the same.
Similarly, again rotate about X and measure the angle formed between the two dotted lines, when the original figure and the traced copy again look just the same.
We find that the measure of the angle is 120°. i.e., we get the same figure after a rotation of 120° – 60° = (60°) about X.
And this will happen six times upto a complete rotation.
Therefore, the order of rotational symmetry of the figure about point X is 6. Also, angle of a complete rotation = 360°
Angle after first overlapping of the original figure and the traced copy = 60° and 360°/60° = 6 = Rotational order.
 Note:
Note:
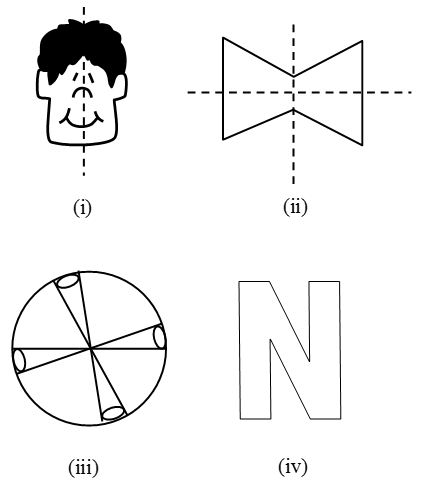
Some shapes have both lines (line symmetry & Rotational symmetry)
Eg.
| Fig. No. | Line Symmetry | Number of Lines of Symmetry | Rotational Symmetry | Order of Rotational Symmetry |
| (i) | Yes | 1 | Yes | 1 |
| (ii) | Yes | 2 | Yes | 2 |
| (iii) | Yes | 4 | Yes | 4 |
| (iv) | No | 0 | Yes | 2 |
