What factors affect the rate of a reaction?
Factors Affecting the Rate of Reaction:
The rate of a chemical reaction can be altered by changing the reacting conditions.
There are five factors that affect the rate of a reaction:
- Total surface area of a solid reactant or particle size of a solid reactant
- Concentration of a reactant in solution
- Temperature of a reaction
- Use of catalyst
- Pressure for a reaction involving gaseous reactants
Table shows some examples of changing the reacting conditions which affect the rates of reactions in our daily occurrences.
| Example | Explanation | Factor affecting the rate |
| (a) It is easier to start a fire using sticks rather than logs | This is because sticks have a bigger total exposed area than the logs. Hence, the rate of burning the sticks is higher than that of the logs. | Surface area (or particle size) |
| (b) Blowing air over glowing charcoal causes it to ignite brightly and quickly | This is due to increase in the concentration of oxygen/air. So, the rate of burning increases. | Concentration |
| (c) Milk turns sour faster on hot days than on cold days | On hot days, the temperature is higher. So, the rate of the milk turns sour is higher. | Temperature |
| (d) The presence of amylase in the saliva breaks starch to maltose | Amylase, as a biological catalyst/enzyme, speeds up the breakdown of starch to maltose. | Catalyst |
| (e) The manufacture of ammonia gas is carried out at high pressure N2(g) + 3H2(g) → 2NH3(g) | At high pressure of the gaseous reactants, the rate of reaction is higher. | Pressure |
People also ask
- What is the rate of the reaction?
- How do you calculate the reaction rate?
- How does the surface area affect the rate of reaction?
- Explain the effect of concentration on the rate of reaction?
- How does the temperature affect the rate of a chemical reaction?
- What is the effect of a catalyst on the rate of a reaction?
- What is the collision theory in chemistry?
- How does the collision theory affect the rate of reaction?
Application of factors that affect the rate of reaction
Application of the factors affecting the rate of reaction in daily life:
- Knowledge of the factors affecting the rate of reaction can be applied to control the rates of many reactions that occur in our daily life.
- These can be done by either speeding up or slowing down the reaction to suit our needs.
Table shows a few examples of applying the factors affecting the rate of reaction to control the rates of a few reactions in our daily life.
| Example | Explaining the effect on the rate of reaction | Factor affecting the rate of reaction |
| (a) Burning of charcoal | Food can be cooked faster when smaller pieces of charcoal are used compared to bigger pieces of charcoal. This is because smaller pieces of charcoal have a larger total exposed surface area compared to bigger pieces. Hence, smaller pieces of charcoal can burn faster to produce more heat per second and the food is cooked faster. | Surface area of charcoal that controls its rate of burning |
| (b) Storing of food in a refrigerator | The decaying and decomposition of food by microorganisms are chemical reactions occurring in food that cause the food to turn bad. When the food is kept in a refrigerator, the food lasts longer. This is because the low temperature in the refrigerator slows down the decaying and decomposition of food by microorganisms. | Temperature that controls the rate of decaying of food by microorganisms |
| (c) Cooking of food in a pressure cooker | In a pressure cooker, the high pressure raises the boiling point of water to a temperature above 100°C. Thus, cooking is carried out at a temperature higher than 100°C in the pressure cooker. The higher temperature increases the rate of cooking. Hence, the food can be cooked faster. | Temperature that controls the rate of cooking |
| (d) Cooking of solid food with different sizes | Solid food in big chunks such as big chunks of potato have a smaller total surface area exposed to heat during cooking. Hence, the food will be cooked at a lower speed. For the food to be cooked faster, the big chunks of solid food must be cut into smaller pieces such as potato chips to increase its total surface area exposed to heat. | Surface area that controls the rate of cooking |
Application of the factors affecting the rate of reaction in industrial processes
- Knowledge of the factors affecting the rate of reaction is applied in choosing the optimum conditions to run an industrial process to achieve
(a) shorter time of production
(b) higher yield
(c) lower cost of production - It is very costly to run an industrial process at a very high temperature and pressure.
- Catalysts are generally used to increase the rates of these processes.
- The catalysts used enable the processes to be run in a shorter time at an optimum temperature and pressure to reduce the cost of production.
Three examples of industrial processes are:
(a) Haber Process
- Haber process is an industrial process to manufacture ammonia on a large scale. In this process, nitrogen reacts with hydrogen to produce ammonia.
- Table describes the effect of catalyst, temperature and pressure on the rate of production of ammonia and its yield.
| Factors | Effect on the rate of reaction | Effect on the yield of ammonia | Conditions chosen |
| Catalyst | The use of catalyst increases the rate of production of ammonia | The quantity of ammonia (yield) produced remains the same with or without the catalyst | Iron is used as a catalyst to increase the rate of production of ammonia |
| Temperature | Increase in temperature will increase the rate of production of ammonia | Increase in temperature will decrease the quantity of ammonia (yield) produced | An optimum temperature of 450 to 550°C is chosen. A compromise is reached for a reasonable rate and yield. |
| Pressure | Increase in pressure will increase the rate of production of ammonia | Increase in pressure will increase the quantity of ammonia (yield) produced. | A high pressure of 200 to 300 atm is chosen to obtain a higher rate and yield. |
- So, Haber process is run in the industry as below:
In the Haber process, a mixture of nitrogen gas and hydrogen gas in the volume ratio of 1:3 is passed over iron powder (catalyst) at a temperature of 450 to 550°C and a pressure of 200 to 300 atm in the presence of molybdenum as a promoter.
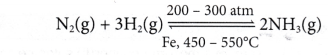
- These optimum conditions enable the Haber process to run at a higher rate to cut down the cost and time of production, and also to obtain a higher yield.
(b) Ostwald Process
- Ostwald process is an industrial process to manufacture nitric acid on a large scale.
- Ostwald process involves three stages, as shown in Table.
| Stage | Reacting conditions | Chemical equation for the reaction |
| I | Ammonia gas is mixed with excess air and the mixture is passed over platinum (catalyst) at a temperature of 850°C and a pressure of 2 to 5 atm. Ammonia is oxidised to nitrogen monoxide. All these reacting conditions are chosen to ensure the reaction occurs at an optimum rate with an optimum yield. | 4NH3(g) + 5O2(g) → 4NO(g) + 6H2O(l) |
| II | Nitrogen monoxide gas from stage I is then reacted with excess air to produce nitrogen dioxide gas. | 2NO(g) + 02(g) → 2N02(g) |
| III | Nitrogen dioxide gas from stage II is then mixed with excess air and dissolved in hot water at 80°C to produce nitric acid | 4NO2(g) + O2(g) + 2H2O(l) → 4HNO3(aq) |
(c) Contact process
- Contact process is an industrial process to manufacture sulphuric acid on a large scale.
- Contact process involves four stages, as shown in Table.
| Stage | Reacting conditions | Chemical equation for the reaction |
| 1 | Sulphur is burnt in excess air to produce sulphur dioxide gas | S(s) + O2(g) → SO2(g) |
| II | Sulphur dioxide gas from stage 1 is mixed with excess air and the mixture is passed over vanadium(V) oxide, V2O5 (catalyst) at a temperature of 450°C and a pressure of 1 atmosphere. Sulphur dioxide is oxidised to sulphur trioxide. All these reacting conditions are chosen to ensure the reaction occurs at an optimum rate with an optimum yield. | 2SO2(g) + O2(g) → SO3(g) |
| III | Sulphur trioxide gas from stage II is then dissolved in concentrated sulphuric acid to form a liquid called oleum, H2S2O7. | SO3(g) + H2SO4(aq) → H2S2O7(l) |
| IV | The oleum from stage III is then diluted with water to produce concentrated sulphuric acid of about 98%. | H2S2O7(l) + H20(l) → 2H2SO4(aq) |
Factors affecting the rate of reaction problems with solutions
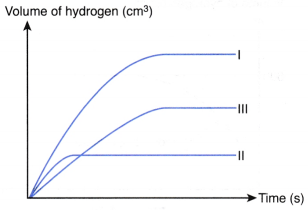
1. Table shows the reacting conditions for three sets of experiments.
| Set | Reacting condition |
| I | 5 g of excess zinc powder + 100 cm3 of 0.4 moi dm-3 sulphuric acid + 5 cm3 of 1 mol dm–3 copper(ll) sulphate solution at room temperature |
| II | 5 g of excess zinc powder + 50 cm3 of 0.4 mol dm-3 sulphuric acid at room temperature |
| III | 5 g of excess granulated zinc + 75 cm3 of 0.4 mol dm–3 sulphuric acid at room temperature |
Sketch the graphs of the volume of hydrogen gas liberated against time for sets I, II and III on the same axes. Explain how you obtain your answers.
Solution:
1. Compare the yield

From the table, number of moles of sulphuric acid reacted in set I > set III > set II.
Thus, the maximum volume of hydrogen gas liberated in set I > set III > set II.
2. Compare the rate

- Initial rate of reaction for set I > set II because of the presence of catalyst in set I.
- Initial rate of reaction for set II > set III because the total surface area of zinc used in set II is larger than that in set III.
- Hence, the initial rate of reaction for set I > set II > set III
- This means that the initial gradient of the curve for set I > set II > set III.
3. Sketch the graph
The graphs for the three sets of the experiments are:
2. 5 g of excess marble chips is added to 80.0 cm3 of 1.0 mol dm–3 acid R in a conical flask. The conical flask is placed on an electronic balance. The mass of the conical flask and its contents is recorded at regular time intervals. Figure shows the graph of the mass of the conical flask and its contents against time.
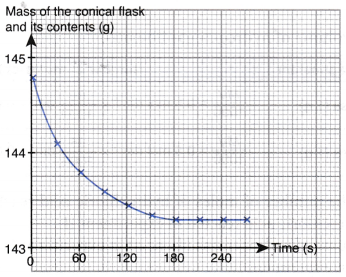
(a) Write the chemical equation for the reaction if acid R is ethanoic acid.
(b) Why does the curve become horizontal after 180 s?
(c) (i) Describe the change in the rate of reaction during the first 180 s. Explain how you derive your answer from the graph.
(ii) Explain the change in the rate of reaction in (c)(i).
Solution:
(a) CaCO3(s) + 2CH3COOH(aq) → Ca(CH3COO)2(aq) + CO2(g) + H2O(l)
(b) The reaction has stopped after 180 s because all the acid R has reacted completely with excess marble.
(c) (i) Rate of reaction decreases with time during the first 180 s. This is because the magnitude of the gradient of the curve decreases with time.
(ii) The concentration of acid R and the total surface area of marble chips decrease with time, hence the rate of reaction decreases with time.
3. 1 g of excess magnesium powder is added to 50 cm3 of 0.5 mol dm–3 hydrochloric acid at room temperature. Figure shows the curve obtained when the volume of hydrogen gas liberated against time is plotted.
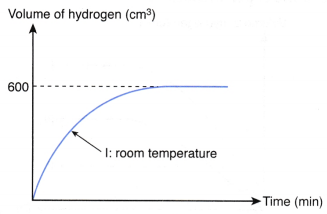
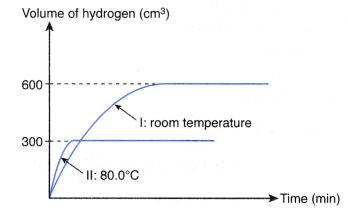
The experiment is repeated using 25 cm3 of 0.5 mol dm–3 hydrochloric acid at 80.0°C to replace 50 cm3 of 0.5 mol dm–3 hydrochloric acid at room temperature. Copy the graph and sketch on the same axes the curve that you would expect to obtain for the second experiment. Explain how you obtain your answer.
Solution:
1. Compare the maximum volume of hydrogen gas liberated

- From the above table, the number of moles of hydrochloric acid reacted in experiment I is twice the number of moles of hydrochloric acid reacted in experiment II.
- Thus, the maximum volume of hydrogen gas liberated in experiment I is twice the maximum volume of hydrogen gas liberated in experiment II.
- Hence, the maximum volume of hydrogen gas liberated in experiment II
= 1/2 x 600 cm3
= 300 cm3
2. Compare the initial rate

- From the above table, the temperature of experiment II is higher than that of experiment I, whereas the other two factors remain constant.
- Hence, the initial rate of reaction of experiment II is higher than that of experiment I.
- In other words, the initial gradient of curve II is steeper than that of curve I.
3. Sketch the curve
Based on the above analysis, the curve for experiment II is shown below.
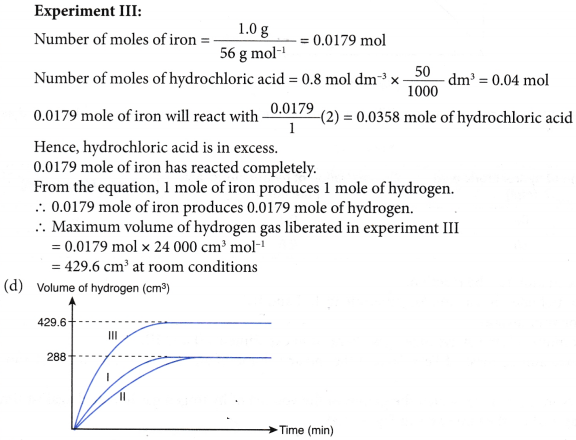
4. Experiment I is carried out to study the rate of reaction between 1.0 g of iron foil with 60 cm3 of 0.4 mol dm–3 hydrochloric acid. The graph in Figure is obtained.
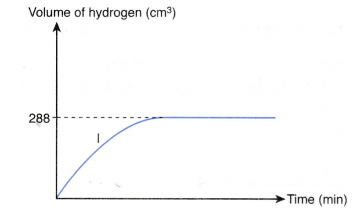
The experiment is repeated two more times using different volumes and concentrations of hydrochloric-acid as shown in Table.

(a) Write the chemical equation for the reaction.
(b) (i) Compare the initial rates of reaction for experiments I, II and III.
(ii) Give reasons for your answers.
(c) Determine the maximum volume of hydrogen gas liberated in experiments II and III.
Given that the relative atomic mass of Fe = 56 and the molar volume of any gas is 24 dm–3 mol–1 at room conditions.
(d) By using the answers in (b) and (c), sketch the graphs of the volume of hydrogen gas liberated against time for experiments II and III on the same axes in Figure.
Solution:
(a) Fe(s) + 2HCl(aq) → FeCl2(aq) + H2(g)
(b) (i) Initial rate of reaction for experiment III > experiment I > experiment II
(ii) This is because the concentration of hydrochloric acid in experiment III > experiment I > experiment II.