Factoring Trinomials (a = 1)
Squaring a binomial creates a perfect square trinomial:
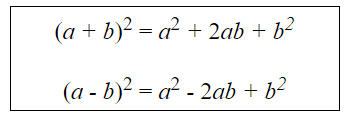
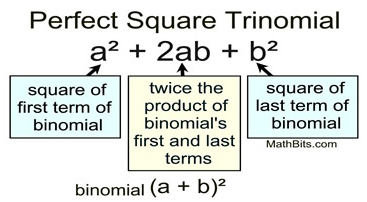
What we need to do now, is to “remember” these patterns so that we can be on the look-out for them when factoring.
Whether we use the distributive process, use FOIL, or line up the factors vertically to multiply, we all know that:
(x + 3) (x – 3) = x2 + x – 6
The expression x2 + x – 6 is called a quadratic trinomial. To factor a trinomial of this form, we need to reverse the multiplication process we used above.
ATTENTION Super Sleuths:
We are on the hunt for factors! There are many different ways to think about this process of “reversing” multiplication. Let’s look first at what is happening and then at a shortcut process for finding the factors.
Example 1: Factor: x2 + 12x + 36
Solution:
Does this fit the pattern of a perfect square trinomial?
Yes. Both x2 and 36 are perfect squares, and 12x is twice the product of x and 6.
Since all signs are positive, the pattern is (a + b)2 = a2 + 2ab + b2.
Let a = x and b = 6.
Answer: (x + 6)2 or (x + 6)(x + 6)
Example 2: Factor: 9a2 – 6a + 1
Solution:
Does this fit the pattern of a perfect square trinomial?
Yes. Both 9a2 and 1 are perfect squares, and 6a is twice the product of 3a and 1.
Since the middle term is negative, the pattern is (a – b)2 = a2 – 2ab + b2.
Let a = 3a and b = 1.
Answer: (3a – 1)2 or (3a – 1)(3a – 1)
Example 3: Factor: (m + n)2 + 12(m + n) + 36
Solution:
This is a sneaky one! Do NOT start by removing the parentheses. Look at the pattern, instead.
Does this fit the pattern of a perfect square trinomial?
Yes. Both (m + n)2 and 36 are perfect squares, and 12(m + n) is twice the product of (m + n) and 6.
Since the middle term is positive, the pattern is (a + b)2 = a2 + 2ab + b2.
Let a = (m + n) and b = 6.
Answer: ((m + n) + 6)2 or (m + n + 6)2
