Factoring by Grouping with a Grid Box
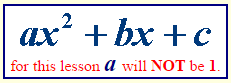
Let’s look at factoring
![]()
This time, let’s use our grouping process written in a grid box.
When “factoring by grouping”, dealing with the signs may be problematic. To avoid this confusion, many students find the creation of a “grid box” to be helpful.
We start, again, by multiply the leading coefficient, a, and the constant term, c.
10 • (-6) = -60
2.
We still consider all of the possible factors of this new product and we find the one pair that adds to the middle term’s coefficient, b. For this example, we need a sum of -11.
4 + -15 = -11
Factors of -60:
(1) • (-60)
(2) • (-30)
(3) • (-20)
(4) • (-15)
(5) • (-12)
(6) • (-10)
(10) • (-6)
(12) • (-5)
(15) • (-4)
(20) • (-3)
(30) • (-2)
(60) • (-1)
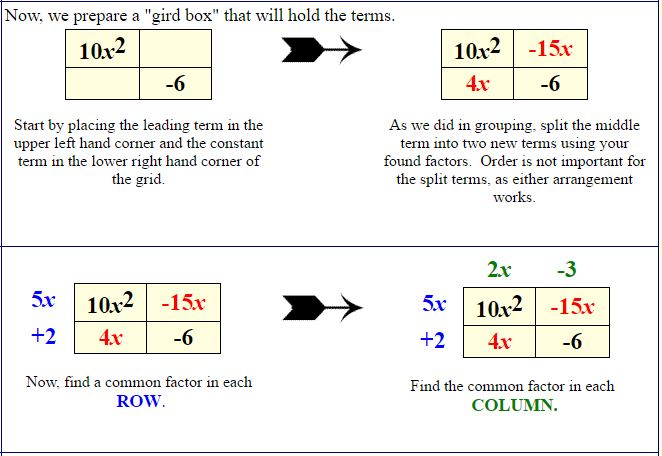
Notice what happens in this example which contains a common factor of 2, that has not been factored out before starting the process.

