Factoring Difference of Two Perfect Squares
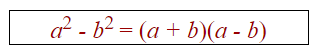
This expression is called a difference of two squares.
(Notice the subtraction sign between the terms.)
In algebra, a term is a perfect square when the numerical coefficient (the number in front of the variable) is a perfect square number, and the exponents of each of the variables are even numbers.
49x2; 25x6; 81y4; 9x2y8; 121x12 are perfect squares.
Remember:
An algebraic term is a perfect square when the numerical coefficient (the number in front of the variables) is a perfect square and the exponents of each of the variables are even numbers.
Example 1: Factor: x² – 9
Both x² and 9 are perfect squares. Since subtraction is occurring between these squares, this expression is the difference of two squares.
What times itself will give x² ? The answer is x.
What times itself will give 9 ? The answer is 3.
These answers could also be negative values, but positive values will make our work easier.
The factors are (x + 3) and (x – 3).
Answer: (x + 3) (x – 3) or (x – 3) (x + 3) (order is not important)
Example 2: Factor 4y2 – 36y6
There is a common factor of 4y2 that can be factored out first in this problem, to make the problem easier.
4y2 (1 – 9y4)
In the factor (1 – 9y4), 1 and 9y4 are perfect squares (their coefficients are perfect squares and their exponents are even numbers). Since subtraction is occurring between these squares, this expression is the difference of two squares.
What times itself will give 1? The answer is 1.
What times itself will give 9y4 ? The answer is 3y2 .
The factors are (1 + 3y2) and (1 – 3y2).
Answer: 4y2 (1 + 3y2) (1 – 3y2) or 4y2 (1 – 3y2) (1 + 3y2)
If you did not see the common factor, you can begin with observing the perfect squares. Both 4y2 and 36y6 are perfect squares (their coefficients are perfect squares and their exponents are even numbers). Since subtraction is occurring between these squares, this expression is the difference of two squares.
What times itself will give 4y2 ? The answer is 2y.
What times itself will give 36y6 ? The answer is 6y3.
The factors are (2y + 6y3) and (2y – 6y3).
Answer: (2y + 6y3) (2y – 6y3) or (2y – 6y3) (2 + 6y3)
These answers can be further factored as each contains a common factor of 2y:
2y (1 + 3y2) • 2y (1 – 3y2) = 4y2 (1 + 3y2) (1 – 3y2)
Example 3: Factor: x2 – 64
Solution:
Both x2 and 64 are perfect squares and this problem is subtraction. It qualifies for use of the difference of squares formula. a2 – b2 = (a + b)(a – b)
x2 is the square of x; 64 is the square of 8. a = x and b = 8
[While -x and -8 are also possible, the positive values will make the work easier.]
Answer: x2 – 64 = (x + 8)(x – 8) or (x – 8)(x + 8)
Example 4: Factor: 9m2 – 81n6
Solution:
First, there is a common factor of 9 in these terms. 9(m2 – 9n6 )
Both m2 and 9n6 are perfect squares and this problem is subtraction. It qualifies for use of the difference of squares formula. a2 – b2 = (a + b)(a – b)
m2 is the square of m; 9n6 is the square of 3n3. a = m and b = 3n3
Answer: 9m2 – 81n6 = 9(m + 3n3 )(m – 3n3 )
Note: This process of factoring does NOT apply to a2 + b2.
