Factor Theorem
Theorem: If p(x) is a polynomial of degree n ≥ 1 and a is any real number, then
(i) x – a is a factor of p(x), if p(a) = 0, and (ii) p(a) = 0, if x – a is a factor of p(x).
Proof: By the Remainder Theorem,
p(x) = (x – a) q(x) + p(a).
(i) If p(a) = 0, then p(x) = (x – a) q(x),
which shows that x – a is a factor of p(x).
(ii) Since x – a is a factor of p(x),
p(x) = (x – a) g(x) for same polynomial g(x).
In this case, p(a) = (a – a) g(a) = 0.
To use factor theorem
- Step 1: (x + a) is factor of a polynomial p(x) if p(–a) = 0.
- Step 2: (ax – b) is a factor of a polynomial p(x) if p(b/a) = 0
- Step 3: ax + b is a factor of a polynomial p(x) if p(–b/a) = 0.
- Step 4: (x – a) (x – b) is a factor of a polynomial p(x) if p(a) = 0 and p(b) = 0.
Factor Theorem Example Problems With Solutions
Example 1: Examine whether x + 2 is a factor of x3 + 3x2 + 5x + 6 and of 2x + 4.
Solution: The zero of x + 2 is –2.
Let p(x) = x3 + 3x2 + 5x + 6 and s(x) = 2x + 4
Then, p(–2) = (–2)3 + 3(–2)2 + 5(–2) + 6
= –8 + 12 – 10 + 6
= 0
So, by the Factor Theorem, x + 2 is a factor of x3 + 3x2 + 5x + 6.
Again, s(–2) = 2(–2) + 4 = 0
So, x + 2 is a factor of 2x + 4.
Example 2: Use the factor theorem to determine whether x – 1 is a factor of
(a) x3 + 8x2 – 7x – 2
(b) 2x3 + 5x2 – 7
(c) 8x4 + 12x3 – 18x + 14
Solution:

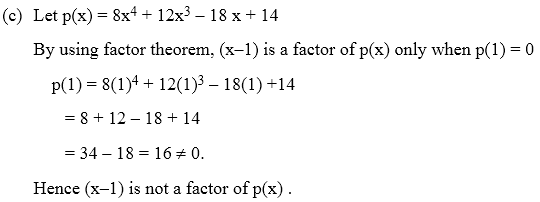
Example 3: Factorize each of the following expression, given that x3 + 13 x2 + 32 x + 20. (x+2) is a factor.
Solution:
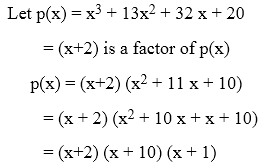
Example 4: Factorize x3 – 23 x2 + 142 x – 120
Solution:
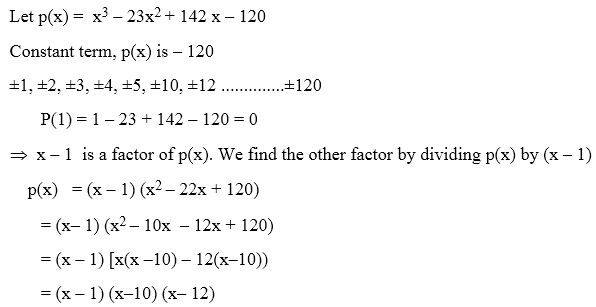
Example 5: Show that (x – 3) is a factor of the polynomial x3 – 3x2 + 4x – 12
Solution:
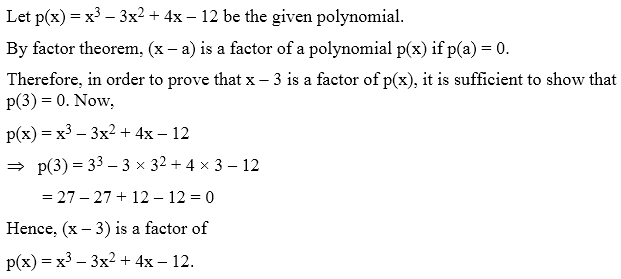
Example 6: Show that (x – 1) is a factor of x10 – 1 and also of x11 – 1.
Solution:
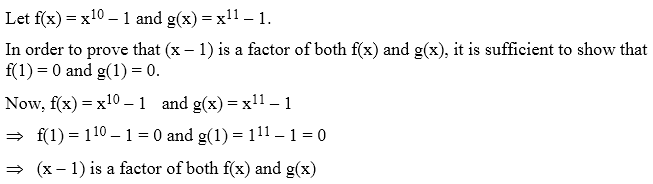
Example 7: Show that x + 1 and 2x – 3 are factors of 2x3 – 9x2 + x + 12.
Solution:

Example 8: Find the value of k, if x + 3 is a factor of 3x2 + kx + 6.
Solution:
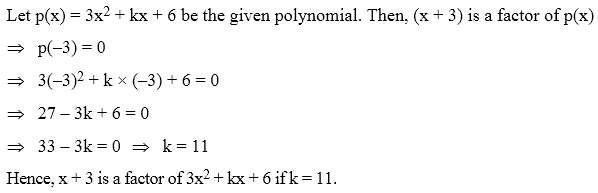
Example 9: If ax3 + bx2 + x – 6 has x + 2 as a factor and leaves a remainder 4 when divided by (x – 2), find the values of a and b.
Solution:

Example 10: If both x – 2 and x – 1/2 are factors of px2 + 5x + r, show that p = r.
Solution:

Example 11: If x2 – 1 is a factor of ax4 + bx3 + cx2 + dx + e, show that a + c + e = b + d = 0.
Solution:

Example 12: Using factor theorem, show that a – b, b – c and c – a are the factors of a(b2 – c2) + b(c2 – a2) + c(a2 – b2).
Solution:

