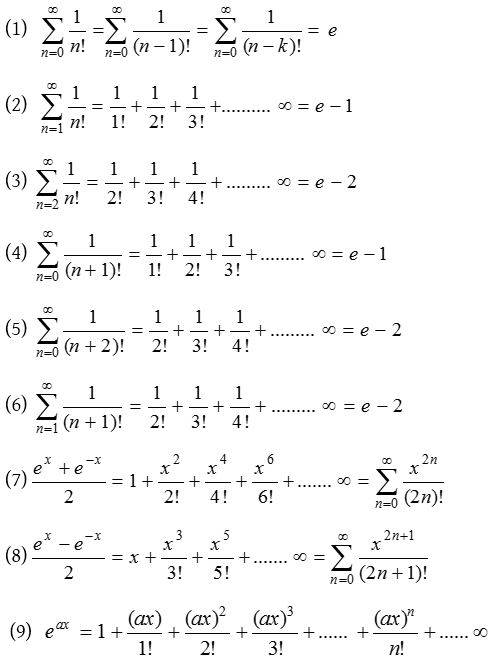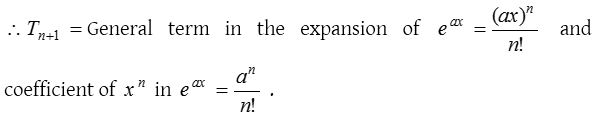Exponential Series
Exponential Series
Definition (The number e)
The limiting value of when n tends to infinity is denoted by e.
Properties of e
(1) e lies between 2.7 and 2.8. i.e., 2.7 < e < 2.8.
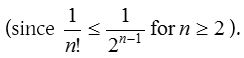
(2) The value of e correct to 10 places of decimals is 2.7182818284.
(3) e is an irrational (incommensurable) number.
(4) e is the base of natural logarithm (Napier logarithm) i.e., ln x = loge x and log10 e is known as Napierian constant. log10 e = 0.43429448, ln x = 2.303 log10 x
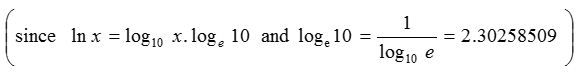
Expansion of exponential series
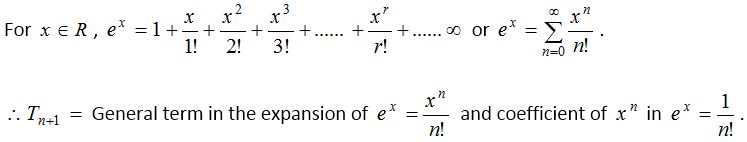
The above series known as exponential series and is called exponential function. Exponential function is also denoted by exp. i.e., ex exp A = eA; ∴ exp x = ex.
Replacing x by -x, we obtain
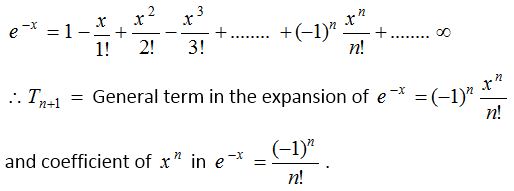
Exponential function ax, where a > 0
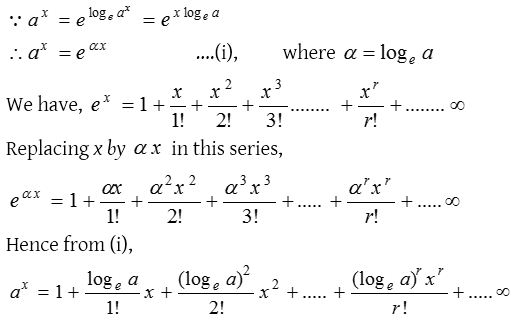
Some standard results from exponential series