Exponential Equations
An exponential equation is one in which a variable occurs in the exponent.
An exponential equation in which each side can be expressed in
terms of the same base can be solved using the property:
\(b^x\) = \(b^y\) then x=y
If the bases are the same, set the exponents equal.
Examples :
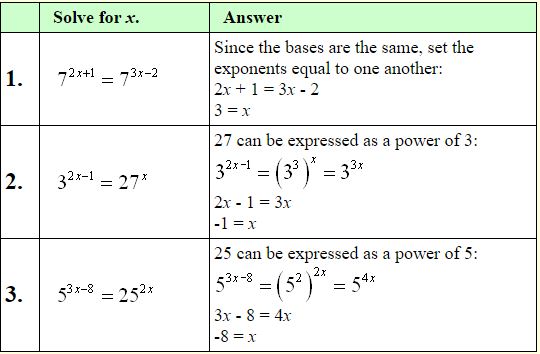
Unfortunately, not all exponential equations can be expressed in terms of a common base. For these equations, logarithms are used to arrive at a solution. (You may solve using common log or natural ln.)
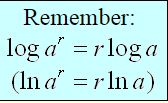
To solve most exponential equations:
1. Isolate the exponential expression.
2. Take log or ln of both sides.
3. Solve for the variable.
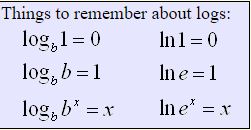

>

