Examples of Applications of Exponential Functions
We have seen in past courses that exponential functions are used to represent growth and decay.
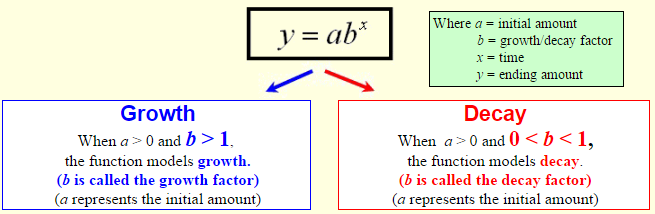
Let’s look at examples of these exponential functions at work.
1. Population: The population of the popular town of Smithville in 2003 was estimated to be 35,000 people with an annual rate of increase (growth) of about 2.4%.
a.) What is the growth factor for Smithville?
After one year the population would be 35,000 + 0.024(35000).
By factoring we see that this is 35,000(1 + 0.024) or 35,000(1.024).
The growth factor is 1.024. (Remember that the growth factor is greater than 1.)
b.) Write an equation to model future growth.
Y = abx = a(1.024)x = 35,000(1.024)x
where y is the population; x is the number of years since 2003
c.) Use your equation to estimate the population in 2007 to the nearest hundred people.
Y = abx = a(1.024)x = 35,000(1.024)x

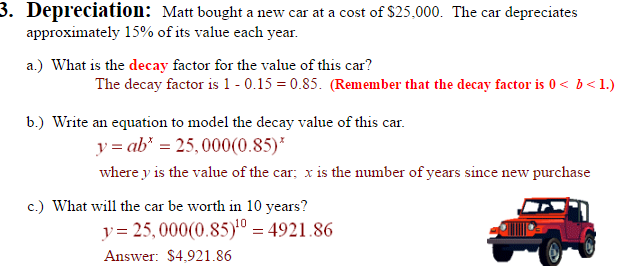
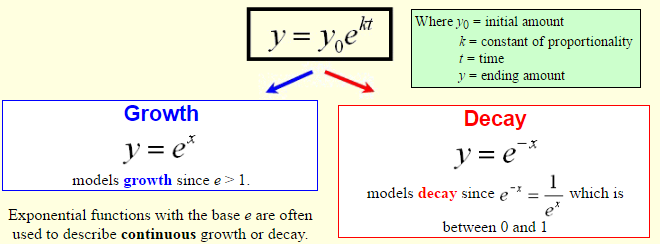

5. Half-Life: Radium-226, a common isotope of radium, has a half-life of 1620 years. Professor Korbel has a 120 gram sample of radium-226 in his laboratory.
a.) Find the constant of proportionality for radium-226.

6. Bacteria Growth: A certain strain of bacteria that is growing on your kitchen counter doubles every 5 minutes. Assuming that you start with only one bacterium, how many bacteria could be present at the end of 96 minutes?

